|
Édition du: 23/10/2024 |
|
INDEX |
Théorème de Pythagore |
|||
![]()
|
Démonstrations avec le produit
scalaire Théorème de Pythagore Les démonstrations vectorielles du
théorème de Pythagore sont souvent accusées de références circulaires:
utilisation implicite du théorème de Pythagore pour se démontrer lui-même.
Pas toujours inéluctable si ces cas sont traités
avec attention ! En l'occurrence, la méthode présentée ici ne se prête à aucune
discussion. Il s'agit d'une construction purement algébrique partant de la
définition du produit
scalaire et de l'orthogonalité. Certains mathématiciens affirment même que cette démonstration est la
meilleure, la plus élégante et finalement pas si compliquée. Elle démontre la puissance de l'algèbre
linéaire. D'autres commentaires à voir in fine. |
||
|
|
Sommaire de cette page >>>
Définition du produit scalaire >>>
Propriétés du produit scalaire >>>
Orthogonalité >>>
Théorème de Pythagore >>>
Commentaire |
Débutants Glossaire |
Voir Types de démonstrations
du théorème de Pythagore
|
On suppose aucune connaissance et aucune référence à la géométrie
euclidienne. Définition du produit scalaire de deux vecteurs Il s'agit d'associer un nombre à deux vecteurs. Notation: un point-milieu entre les deux vecteurs ou
parenthèses spéciales. |
|
|
|
Quadrance Sorte de
carré. |
|
|
|
Bilinéarité Le produit scalaire de trois vecteurs est "distributif". |
|
||
|
Démonstration Soit trois vecteurs. Démonstration de la première égalité, les autres se démontrent sur le
même principe. |
|
||
|
Symétrie "Commutativité". |
|
||
|
Démonstration En algèbre classique les produits sont commutatifs. |
|
||
|
Définition Deux vecteurs sont dits orthogonaux si => Aucune allusion à une disposition géométrique. |
|
|
|
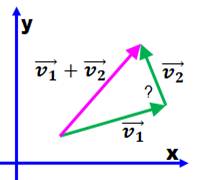
Théorème Pour tous vecteurs v1 et v2 : |
|
|
|
Relation entre les trois vecteurs Addition classique des vecteurs. Quelle est la valeur de l'angle entre les deux vecteurs verts ? |
|
|
|
Implication |
Cette relation prise comme hypothèse est explicitée puis calculée pour
arriver à la conclusion qu'elle implique que les vecteurs sont orthogonaux. |
|
|
Démonstration Expression explicitée puis application de la bilinéarité.
|
|
|
|
Suppression des éléments communs puis application de la symétrie. Division par 2, et Conclusion suite à notre définition de l'orthogonalité. |
|
|
Voir Cette démonstration est exposée dans les deux références citées
Commentaires: est-il possible d'échapper à la référence circulaire ? Il
semble que oui !
|
Il existe certains sujets comme celui-ci
qui offre des débats sans fin sur Internet. Si la démonstration exposée ci-dessus ne
vous convainc pas, je vous propose de vous référer à la vidéo suivante: https://youtu.be/rKSi_fCAxc0 - My Proof of Pythagoras's Theorem is NOT
circular! - MathTheBeautiful Elle est en anglais, mais facile à suivre,
me semble-t-il. Commentaire de Dom
Marro publié avec son autorisation Bonjour, J'ai lu sur votre site votre argumentation
permettant de justifier que la démonstration du théorème de Pythagore par le
produit scalaire est valide et non circulaire. N'étant pas d'accord avec vous sur ce
point, je souhaiterais échanger avec vous sur le sujet pour me permettre de
comprendre en détail votre justification. En effet la définition purement algébrique
du produit scalaire sur un espace vectoriel fait que le dessin de n'importe
quelle base du plan en fait une base orthonormée pour le produit scalaire
canonique définie sur cette base. Pour démontrer le théorème de Pythagore en
utilisant le produit scalaire canonique défini sur une base orthonormée telle
qu'on la dessine en géométrie Euclidienne classique, il faut d'abord
démontrer que la norme associée à ce produit scalaire est bien la longueur au
sens classique et ceci ne peut se démontrer qu'en utilisant le théorème de
Pythagore, d'où la circularité de la démonstration. En attente du plaisir d'en parler avec vous Bien cordialement Dom Marro Une démonstration
reconnue ? En mars 2023, deux lycéens de la
Nouvelle-Orléans, Calcea Johnson and Ne’Kiya Jackson, tous deux au St. Mary’s
Academy à New Orleans, affirment
avoir prouvé le théorème en utilisant la trigonométrie sans recourir au
raisonnement circulaire. D’autres mathématiciens avaient déjà prouvé
la même chose, en utilisant le sinus et le cosinus (de simples ratios dans le
triangle rectangle) pour prouver le théorème de Pythagore sans s’appuyer sur
sin²α + cos²α = 1. Est-ce une conclusion
définitive ? Parmi
les autres démonstrations trigonométriques du théorème qui sont apparues
dans le passé, on trouve celle élaborée par Jason Zimba, alors physicien et
mathématicien au Bennington College, et publiée dans Forum Geometricorum en
2009. Cette démonstration utilisait une identité trigonométrique qui permet
de calculer le cosinus et le sinus d’un angle sans utiliser le théorème de
Pythagore, à condition de connaître les cosinus et les sinus de x et y seuls. Le 26 octobre 2009, Bogomolny a ajouté la
preuve de Zimba sur son site Web, en écrivant : « Elisha Loomis, moi-même et
sans doute beaucoup d’autres avons cru et croient toujours qu’aucune preuve
trigonométrique du théorème de Pythagore n’est possible… J’admets volontiers
avoir tort. » Au fil du temps, Bogomolny a ajouté d’autres preuves trigonométriques
sur le site : une de ces preuves pourrait être écrite en seulement quatre
lignes. La saga montre comment même les
mathématiques les plus simples peuvent nous surprendre. « Je pense que les
mathématiciens ont appris à ne pas prétendre avec audace que quelque chose
est impossible parce que nous avons été trop souvent embarrassés au fil des
ans en le faisant », explique Anderson. Références sur le site
d'Alexander Bogomolny (célèbre auteur américain du site Cut-The-Knot) Pythagorean Theorem: Some False
Proofs. Trigonometric
Proof of the Pythagorean Theorem: Il dit: Elisha Loomis, moi-même et sans doute
beaucoup d’autres croyions et croyons toujours qu’aucune preuve
trigonométrique du théorème de Pythagore n’est possible. Cette croyance découle de l'hypothèse selon
laquelle une telle preuve s'appuierait sur la plus fondamentale des identités
trigonométriques sin²α + cos²α = 1 qui n'est rien d'autre qu'une
reformulation du théorème de Pythagore proprement dit. Ainsi, comme le dit l’argument courant, s’y
fier conduirait inévitablement au cercle vicieux du raisonnement circulaire.
Maintenant, Jason Zimba a montré que le théorème peut être dérivé des
formules de soustraction du sinus et du cosinus sans recourir à sin²α +
cos²α = 1. J'admets volontiers que j'ai tort. La démonstration de
Loomis en bref
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Pythagore/ProdScal.htm |