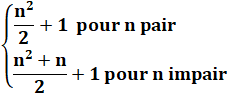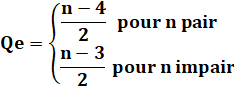|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
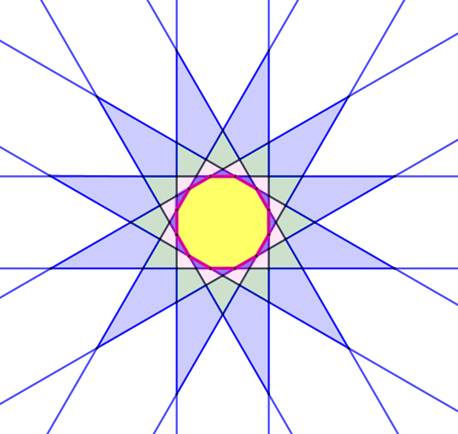
RÉGIONS externes des POLYGONES Régions créées par les droites portant les côtés des polygones Maillage du plan par les
droites prolongeant les côtés des polygones. Quantité de régions créées. |
|
|
||
|
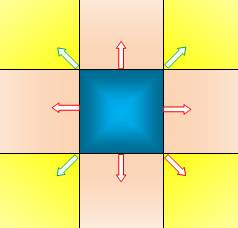
Cas du carré Quelles
sont les régions créées par le dessin d'un carré
(ou d'un rectangle)
sur le plan lorsqu'on prolonge les côtés ? Dénombrement
Bilan: 9 régions dont 1 fermée. |
|
|
|
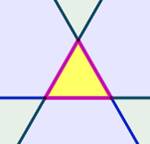
Cas du triangle Même type de dénombrement
Bilan: 7 régions dont 1 fermée. |
|
|
|
|
||
|
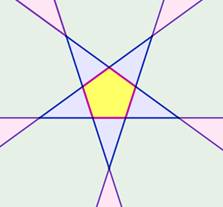
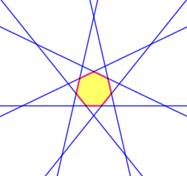
Avec le pentagone
de nouvelles régions font leur apparition. Celles
avec le croisement des droites portant les côtés. Après cette première
intersection, les droites se prolongent sans se croiser à nouveau. Dénombrement
Bilan: 16 régions dont 6 fermées ou bornées. |
|
|
|
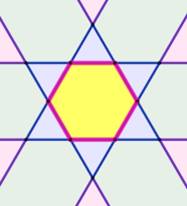
Même type de configuration avec
l'hexagone
Bilan: 19 régions dont 7 fermées ou bornées. |
|
|
|
|
||
|
Avec l'heptagone
encore de nouvelles régions font leur apparition. C'est en
face des sommets que se révèle un nouveau croisement. Dénombrement
Bilan: 29 régions dont 15 fermées ou bornées. |
|
|
|
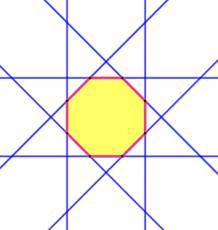
Dénombrement pour l'octogone
Bilan: 33 régions dont 17 fermées ou bornées. |
|
|
|
|
||
|
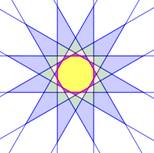
Dénombrement
Bilan: 73
régions dont 49 fermées ou bornées. Figure d'aide au décompte
|
|
|
Voir Brève
545
|
|
||
|
Quantité de régions |
|
|
|
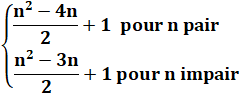
Quantité de régions bornées |
|
|
|
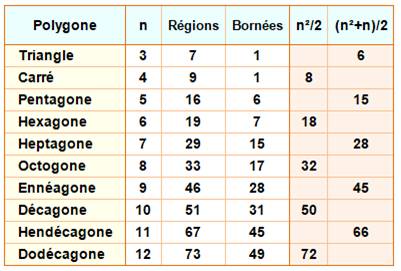
Tableau pour n de 3 à 12 |
|
|
|
Suite donnant la quantité de
RÉGIONS pour n croissant |
7, 9, 16, 19, 29, 33, 46, 51, 67, 73, 92, 99, 121,
129, 154, 163, 191, 201, 232, 243, 277, 289, 326, 339, 379, 393, 436, 451,
497, 513, 562, 579, 631, 649, 704, 723, 781, 801, 862, 883, 947, 969, 1036,
1059, 1129, 1153, 1226, 1251, 1327, 1353, 1432, 1459, 1541, 1569, 1654, 1683,
1771, 1801, … |
|
|
|
|||
|
Prolonger
les faces des polyèdres forme de nouveaux objets: les polyèdres étoilés ou solide de Kepler-Poinsot. En
anglais, ce procédé d'extension des faces se nomme: stellation
(mot qui rappelle stellaire, qui se rapporte aux étoiles) |
Quantité de polygones étoilés
|
||
|
Comme
avec les polygones, en prolongeant les faces des polyèdres, on peut chercher
à savoir:
|
Cas de l'octaèdre régulier et
Octaèdre et régions
Bilan: 59
régions dont 9 fermées. Dodécaèdre et régions Bilan: 122 régions illimitées pour le dodécaèdre, et
? régions fermées (les polyèdres à douze faces sont nombreux). |
||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/PolyRegi.htm
|
![]()