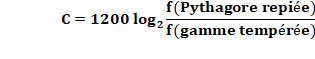|
Édition du: 19/09/2025 |
|
INDEX |
MUSIQUE |
|||
|
Bases de la musique (débutant) |
||||
|
Notes |
Gamme (construction) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES & MUSIQUE Construction de la gamme Comment la gamme
classique (Do, ré, mi, fa, sol, la, si) a été construite. Elle vient de
l'Antiquité … Un montage mathématique
résultant d'une coïncidence numérique:
Ce fait
mathématique est à l'origine de pratiquement toute la théorie musicale : division
de l'octave en douze demi-tons, et rôle primordial de la quinte dans les
accords musicaux. Voir Nombre 128 / Nombre 129,7… |
||
|
|
Sommaire de cette page >>> Enquête du comma: qui est le coupable ? >>> Tableau ce comparaison |
Débutants Glossaire |
|
Enquête du comma: qui est le coupable ? Enquête du célèbre commissaire Matémate
Hique |
||
|
Chapitre 1 – La scène du crime : un clavier
suspect Le commissariat était plongé dans un silence pesant, seulement troublé par
le froissement des feuilles de dossiers. Au centre de la pièce, trônait un
piano droit, noir, lustré, que l’on avait apporté comme pièce à conviction.
Le commissaire Matémate, célèbre pour résoudre des affaires impossibles grâce
à sa passion des mathématiques, faisait les cent pas. Il s’arrêta, fixa les touches du clavier. — Voilà le mystère, dit-il. Pourquoi donc ces touches blanches et noires
alternées de manière irrégulière ? Deux noires, puis trois noires, avec des
espaces différents… et ce long alignement de blanches… Qui a pu concevoir une
telle structure ? Ses inspecteurs, un peu perplexes, se contentèrent de hausser les
épaules. Pour eux, ce n’était qu’un instrument. Pour Matémate, c’était une
scène de mystère mathématique. — Rien n’est laissé au hasard, poursuivit-il. Ces touches révèlent une
logique cachée. Si je découvre qui l’a mise en place, je résoudrai l’énigme
de la gamme de do majeur et de son comma. |
Il sortit un
carnet quadrillé, son "arme" favorite, et y inscrivit les lettres :
Do, ré, mi, fa, sol, la, si. Puis il
entoura en rouge les intervalles, cherchant un indice, comme un détective
devant un code chiffré. |
|
|
Chapitre 2 – L’ombre de Pythagore Matémate savait où chercher. Tout le menait vers un homme qui, bien avant
que les pianos n’existent, avait déjà mené sa propre enquête sonore : Pythagore. Dans son esprit, Matémate reconstitua la scène antique. Pythagore, un soir,
tendant l’oreille devant des forgerons martelant l’enclume. Certaines frappes
semblaient s’accorder entre elles, d’autres juraient. Intrigué, le philosophe
tendit des cordes, les pinça, puis remarqua quelque chose : lorsqu’une corde
était divisée en deux, le son produit
résonnait parfaitement avec l’original. — L’octave, murmura Matémate en notant
dans son carnet: Rapport 2:1. Ce qui
veut dire que deux fois plus longue ou deux fois plus courte, la corde chante
à l’unisson supérieur ou inférieur. Puis, Pythagore fit d’autres expériences : il divisa la corde en rapports
simples. Lorsqu’elle vibrait aux deux tiers de sa longueur, le son obtenu se
mariait avec le premier. C’était la quinte.
Rapport 3:2, conclut Matémate. L’oreille humaine aime les rapports simples entre nombres
entiers. Voilà la clé. |
Matémate
griffonna : Indice
n°2 : Les sons harmonieux obéissent à des
rapports simples. Pythagore aimait les nombres entiers… et les sons purs. |
|
|
Chapitre 3 – Le jeu des quintes et des octaves Dans son École, Pythagore ne se contentait pas de philosopher. Il expérimentait.
Sur ses pas, Matémate, corde tendue à la main, compare les sons comme un
enquêteur compare des empreintes. Il découvre que Pythagore avait eu une idée lumineuse: monter de quinte en quinte :
do → sol → ré → la → mi… et ainsi de suite. Chaque fois, il multipliait la fréquence par 3/2. Et là, il fit une
découverte troublante : 15 quintes empilées donnaient presque exactement 7
octaves. Presque… mais pas tout à fait. Il y avait un minuscule écart, une faille dans le système, que les
musiciens appelleraient plus tard le comma pythagoricien. |
Matémate nota
: Indice
n°3 : 15 quintes ≈ 7 octaves.
Mais l’égalité parfaite n’existe pas. Il faut choisir comment répartir
l'écart. |
|
|
Chapitre 4 – Le repli des quintes En feuilletant les archives, Matémate retrouva la méthode exacte imaginée
par Pythagore. Le philosophe, toujours pragmatique, avait eu une idée de
génie : replier les quintes
dans l’espace d’une seule octave. En effet, chaque fois qu’il multipliait la fréquence d’une note par le
rapport 3/2 — celui d’une quinte parfaite — le son montait, dépassant souvent
la limite de l’octave de départ. Pour le ramener dans cette octave, il
divisait alors la fréquence par 2, autant de fois que nécessaire. En partant d’un do et en montant ainsi de quinte en quinte, tout en
repliant chaque nouvelle note dans l’octave initiale, Pythagore obtint sept
notes distinctes: do, ré, mi, fa, sol, la, si. Cette suite formait une gamme
agréable, équilibrée… mais pas parfaite : les quintes et les octaves ne
coïncidaient pas exactement. Pour corriger cette imperfection, les musiciens inventèrent plus tard la gamme tempérée, divisant l’octave en 12
demi-tons égaux. Matémate comprit alors : les touches blanches du piano correspondent à
ces sept notes de base, tandis que les touches noires représentent les
altérations, indispensables pour jouer dans toutes les tonalités. |
Matémate
poursuit ses notations : Indice
n°4 : La gamme de do majeur est née du
pliage des quintes dans une octave et en retouchant la répartition pour
obtenir douze intervalles égaux. |
|
|
Chapitre 5 – Interrogatoire des suspects : Dièse
et Bémol (Deux
silhouettes pénètrent dans la salle d’interrogatoire. L’une est fine, acérée,
presque tranchante : Dièse. L’autre est ronde, pesante, presque floue :
Bémol. Face à eux, le commissaire Matémate ajuste ses lunettes et ouvre son
carnet.) Matémate : Vous deux… qui êtes-vous vraiment
? Dièse (sifflant) : Je suis l’ascension. J’ajoute un
demi-ton à une note. Ré devient ré♯, fa devient fa♯. Je suis le pas vers l’aigu. Bémol (voix grave) : Moi, je rabaisse. J’enlève un
demi-ton. Si devient si♭, mi devient mi♭. Je suis le glissement vers l’ombre. Matémate (note dans son carnet) : Donc vous êtes des doublons
? Des alias ? Dièse : Pas tout à fait. Parfois, nous
désignons le même son — fa♯ et sol♭, par exemple. Mais selon le contexte, l’un
de nous est préféré à l’autre. Bémol (ricane) : Nous sommes les touches noires du piano.
Sans nous, pas de modulation, pas de tension, pas de mystère. Matémate (regarde son clavier) : C’est donc vous qui occupez
ces groupes de deux et trois, coincés entre les blanches. Un rôle discret…
mais indispensable. |
Indice
n°5 : La gamme de do majeur,
apparemment simple, cache des zones d’ombre. En ajustant les fréquences, les
touches noires — dièses ou bémols — prennent leur place sur le clavier. Elles
ne sont ni doublons ni intrus, mais les agents secrets de la modulation, de
l'altération. |
|
|
Chapitre 6 – Le verdict Matémate
s'empresse de résumer dans son carnet:
Alors,
finalement, il tente une synthèse: L'intervalle
de douze quintes représente une étendue légèrement supérieure à sept octaves,
la différence étant le comma
pythagoricien. Lorsque la dernière quinte est raccourcie pour donner à
l'ensemble une étendue valant exactement sept octaves : elle forme la quinte
dite « du loup » car elle est très
dissonante … La gamme tempérée est une solution; il y en a d'autres ! |
Matémate
sourit. Il avait
résolu l’énigme, mais savait qu’il restait d’autres mystères : le tempérament
égal, les gammes exotiques, les micro-intervalles… Pour
l’instant, il se contenta de poser ses doigts sur le clavier et de jouer un
do majeur. La vérité,
pensa-t-il, peut parfois se résumer à sept notes bien placées. |
|
|
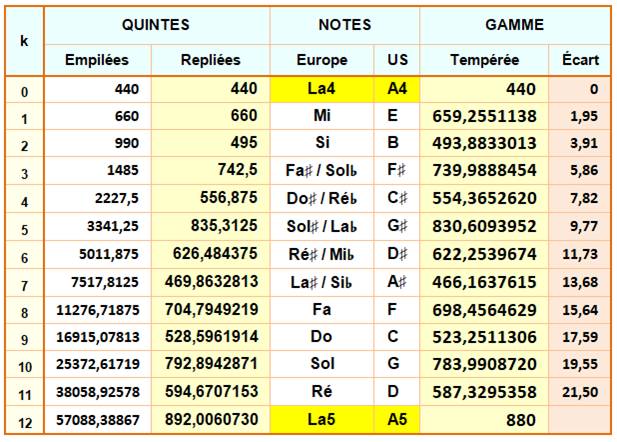
Gamme pythagoricienne et gamme
tempérée
|
||
|
Lecture |
|
|
|
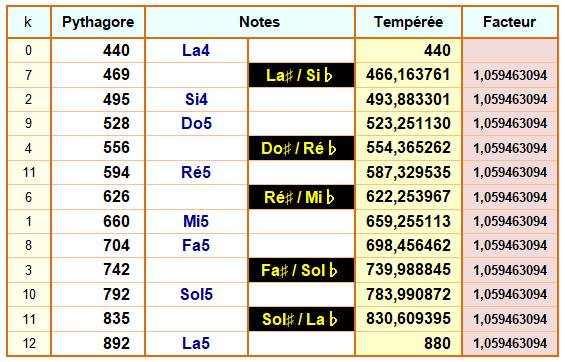
Gamme tempérée Reprises des notes vues ci-dessus, remises dans l'ordre habituel de la
gamme. Notez la nouvelle position de l'indice k. |
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/CultureG/aaaMusiq/MusGamme.htm |