|
Édition du: 17/09/2025 |
|
INDEX |
MUSIQUE |
|||
|
Bases de la musique (débutant) |
||||
|
Notes |
Gamme (construction) |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Introduction Quand les
maths rencontrent la musique. Des touches du piano au rythme d’une fugue de Bach,
des découvertes de Pythagore aux créations par intelligence artificielle, les
mathématiques se cachent derrière chaque note. Cette
page montre comment chiffres et sons s’accordent pour créer l’art universel
qu’est la musique. |
||
|
|
Sommaire de cette page >>> Les notes du
piano et la gamme >>> Gammes:
Pythagore et tempérée >>> Le solfège :
un art et une science >>> Bach et les
mathématiques musicales >>> Mathématiques,
numérique et IA Quelques précisions techniques >>> Touches du
piano >>> Pourquoi sept
blanches et cinq noires >>> Octave et
quinte |
Débutants Glossaire |
|
Tons Un piano possède 88 touches, blanches et noires,
qui représentent les notes de la musique. Les touches blanches correspondent aux notes
naturelles : do, ré, mi, fa, sol, la, si. Les touches noires sont les altérations : dièses (#) ou bémols
(♭). La distance entre deux notes peut être d’un ton (deux demi-tons) ou d’un demi-ton (distance la plus courte
entre deux touches voisines). |
Gamme Une gamme est
une suite de notes organisées selon un schéma précis de tons et demi-tons. La gamme majeure de
do, par exemple, suit: ton –
ton – demi-ton – ton – ton – ton – demi-ton. Référence Pour accorder les instruments, on utilise une
note de référence : le La 440 Hz. Cela
signifie que la corde ou la touche qui produit ce La vibre 440 fois par
seconde. Cette norme internationale permet à tous les
musiciens de jouer ensemble, même s’ils viennent de pays différents. |
|
|
Gamme de Pythagore Dans l’Antiquité, le philosophe grec Pythagore
découvre que les sons agréables sont liés à des rapports simples entre
longueurs de cordes. Par exemple, une corde deux fois plus courte produit un
son une octave plus haute. En enchaînant ces rapports, il construit une
gamme basée sur des quintes parfaites
(rapport 3/2). Cependant, cette gamme de Pythagore présente un problème : quintes et octaves ne
coïncident pas parfaitement. Le petit écart s’appelle le comma pythagoricien.
Il provoque des désaccords dans certaines tonalités, donnant naissance à la
fameuse gamme du loup,
où certaines notes sonnent faux. |
Gamme tempérée Pour résoudre ce problème, les musiciens ont
inventé la gamme
tempérée. Dans ce système, l’octave est divisée
régulièrement en 12 demi-tons égaux. Chaque note est ainsi légèrement ajustée pour que
toutes les tonalités soient jouables avec la même justesse. C’est ce système qu’utilisent aujourd’hui les
pianos et la plupart des instruments modernes. La gamme tempérée est un compromis : elle
sacrifie la pureté parfaite de certains intervalles pour offrir une
flexibilité totale. C’est grâce à elle qu’un pianiste peut passer de do
majeur à si majeur sans réaccorder son instrument. |
|
|
Solfège Le solfège
est le langage écrit de la musique. Il permet de noter les hauteurs (notes), les durées
(rythmes) et les nuances (forte, piano,
crescendo…). Les notes sont placées sur une portée de cinq lignes,
avec des clés (de sol, de fa, d’ut) qui indiquent la position des sons. Mais le solfège n’est pas qu’un art : il repose
sur des notions mathématiques. Les rythmes, par exemple, sont divisés en
fractions : une ronde dure quatre temps, une blanche deux, une noire un, une
croche un demi-temps, etc. Les mesures
organisent ces temps en groupes réguliers (2/4, 3/4, 4/4…). |
Harmonie Les intervalles
entre notes peuvent aussi être mesurés en fréquences (hertz) et en rapports
numériques. Les compositeurs utilisent ces rapports pour
créer des harmonies agréables ou surprenantes. Apprendre le solfège, c’est donc apprendre à lire
et écrire la musique comme on lit et écrit une langue. Cela demande de la rigueur, mais ouvre la porte à
toutes les musiques, du classique au jazz, du rock à la pop. C’est un outil
universel qui relie les musiciens à travers le temps et l’espace. |
|
|
Perfection Johann Sebastian Bach (1685-1750) est souvent considéré comme le maître absolu de
la musique mathématique. Ses œuvres, comme L’Art de la fugue ou Le
Clavier bien tempéré, sont construites avec une précision géométrique. Bach utilisait des fugues, où un thème est répété, inversé, transposé, superposé à
lui-même, créant un tissage sonore complexe. Il jouait avec les symétries : un motif pouvait être lu
à l’endroit, à l’envers, ou même en miroir. Le rythme chez Bach est également très structuré
: il superpose plusieurs motifs rythmiques, créant des effets de polyrythmie. Ses compositions sont comme des puzzles sonores
où chaque pièce s’emboîte parfaitement.. |
Beauté Pourtant, cette rigueur n’enlève rien à
l’émotion. Bach savait que les mathématiques pouvaient
servir la beauté et l’expression. Ses œuvres prouvent que la logique et la
sensibilité peuvent coexister harmonieusement. Aujourd’hui encore, ses partitions fascinent
autant les musiciens que les mathématiciens. Elles sont étudiées non
seulement pour leur beauté musicale, mais aussi comme exemples de structures
mathématiques appliquées à l’art. |
|
|
Le numérique Aujourd’hui, les mathématiques sont partout dans
la musique moderne. Les logiciels de composition utilisent des algorithmes
pour générer des sons, ajuster la justesse, ou créer des effets. Les formats numériques (MP3, WAV) reposent sur
des calculs complexes de compression
et d’échantillonnage. Les synthétiseurs
produisent des sons en manipulant des ondes (sinusoïdales, carrées,
triangulaires) grâce à des formules mathématiques. Les boîtes à rythmes programment des séquences
précises, mesurées en battements par minute (BPM). |
La révolution de l'IA L’intelligence artificielle va
encore plus loin : elle peut analyser des milliers de chansons pour en
composer de nouvelles, imiter le style d’un artiste, ou accompagner un
musicien en temps réel. Des IA peuvent même improviser en suivant les
règles harmoniques et rythmiques. Les mathématiques permettent aussi de visualiser
la musique : spectrogrammes, analyses fréquentielles, modélisations 3D des
sons. Pour les jeunes musiciens, comprendre ces bases
ouvre des possibilités infinies : créer sa propre musique électronique,
programmer des rythmes originaux, ou collaborer avec une IA pour inventer de
nouveaux styles. La rencontre entre art et science n’a jamais été
aussi riche qu’aujourd’hui. |
|
![]()
Précisons techniques
|
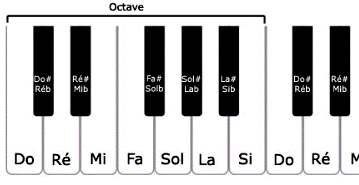
Une octave D’un do au prochain do (non compris), on compte :
Tons et demi, tons L’octave comprend douze demi, tons, chacun représenté par
une touche blanche ou une touche noire, Pour les blanches, on a donc la succession des notes :
Do, Ré, Mi,
Fa, Sol, La, Si Gamme de Do Majeur Pourquoi cette bizarrerie ? Pourquoi une telle gamme
en Do Majeur ? Une composition qui a pris naissance
avec Pythagore et qui a été altérée pour qu'elle sonne bien à l'oreille. |
Le clavier du piano
Gamme du Do Majeur Les touches blanches sont les 7 notes de la gamme majeure (Do, Ré, Mi, Fa, Sol, La, Si). Les touches noires comblent les demi-tons manquants dans cette structure (par ex. Do♯ entre Do et Ré). |
|
|
Touches blanches La gamme diatonique (do-ré-mi-fa-sol-la-si) comporte sept notes, et cette
structure est ancienne,
remontant à la musique grecque et médiévale. Elle est fondée sur des critères
harmoniques
et culturels,
mais aussi mathématiques. Voici comment on peut la voir mathématiquement :
En construisant des quintes successives et en les ramenant (par division)
dans la même octave, on tombe sur sept notes distinctes
dans l’octave. C’est ce qu’on appelle le cycle des quintes restreint à sept
étapes. Ce système forme la base de la gamme
majeure. |
Touches noires La gamme diatonique n’utilise
que sept des douze demi-tons possibles. Pourtant, l’échelle
des sons (en fréquence) permet douze
hauteurs différentes dans l’octave si on divise l’octave en
demi-tons égaux : c’est ce qu’on appelle la gamme chromatique (do, do♯, ré,
ré♯, mi, etc.). Les dièses
(ou bémols) ont été introduits progressivement dans l’histoire
de la musique pour enrichir les possibilités harmoniques. Mais la base de la musique reste la gamme de sept notes,
car elle reflète une organisation plus naturelle des intervalles perçus comme
consonants. |
|
|
Le piano est un compromis
visuel et pratique :
|
||
|
|
Harmoniques et série harmonique
Intervalles: choix pour construire une gamme
Suite sur les intervalles >>>
|
|||||||||||||||||||||
Suite avec Enquête
du commissaire Métamate: construction de la gamme

Voir Vocabulaire des maths et de
la musique
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/CultureG/aaaMusiq/MusBases.htm |