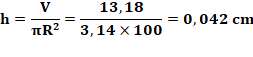NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/03/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Physiques
Débutants Général	BASES – Hydrostatique					Glossaire Général
INDEX Sciences	Archimède – Débutant		Principe d'Archimède	Pompage
			La couronne en or
		Sommaire de cette page Euréka d'Archimède >>> Approche >>> Histoire >>> Légende >>> Poussée d'Archimède >>> Théorème d'Archimède

La couronne en or et Archimède

Archimède doit trouver si la couronne en or est frelatée et cela sans la corrompre.

Les deux versions de l'expérience:

Comparaison de volumes

Pesée dans l'eau (Comme illustré sur ce timbre)

Source image: Stock Photo - Greece - Circa 1983 A stamp printed in Greece from the Europa issue

showing ancient Greek mathematician and physicist Archimedes of Syracuse – 123RF

Approche
EURÊKA interjection; du grec hêurêka, j'ai trouvé. Exclamation attribuée à Archimède découvrant dans son bain la poussée des liquides sur les corps immergés; Parole de contentement qu'on emploie lorsqu'on trouve brusquement une solution, une bonne idée; ex: Eurêka! j'ai la solution.  Larousse

La petite histoire!

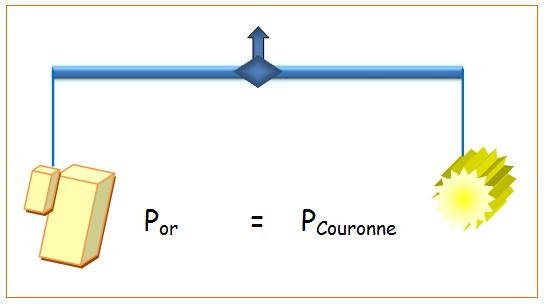
Le roi de Syracuse Hiéron II de Syracuse (306-214) se fait faire une couronne en or en fournissant la quantité d'or nécessaire. L'orfèvre lui présente la couronne ainsi réalisée. Très bien! Mais le roi a un doute et voudrait savoir si l'orfèvre a bien utilisé tout l'or; s'il n'en a pas escamoté une partie. La pesée montre que la couronne a bien le même poids que l'or fournit au départ. Mais est-ce suffisant? Le roi confie le problème à Archimède.

Ce qui est suspecté: que l'orfèvre ait remplacé de l'or par de l'argent qui a moins de valeur et que celui-ci se soit arrangé pour obtenir le poids correspondant au poids de l'or fourni par le roi.

Oui, mais alors, l'argent et l'or n'ayant pas la même masse volumique, s'il y a fraude, le volume doit être plus grand.

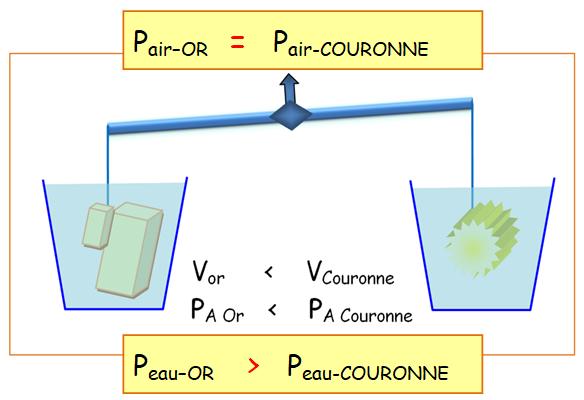
Or: 19,3 kg pour un dcm³ (1 litre) ou 19 300 kg.m^-3

Argent: 10,5

à poids égal, il faut un plus grand volume d'argent que d'or.

Voici donc le problème tel qu'il se pose à Archimède:

Comment déterminer s'il y a eu changement de volume entre

le lingot d'or mis à disposition par le roi et

la couronne telle que fournie par l'orfèvre.

Archimède cogite dans son bain (aux bains publics) en observant des objets qui flottent …

Soudain, il en sort tout joyeux, sans même se soucier de sa tenue vestimentaire et s'écrie: eurêka, eurêka.

Il venait de trouver ce qui est connu aujourd'hui comme le théorème d'Archimède.

Et voilà un moyen astucieux pour comparer des poids en mesurant des volumes.

Archimède (-287 à -212 av. J.-C. - Syracuse) fait l'expérience devant le roi. - Une cuve remplie à ras-bord est placée dans une cuve plus grande et vide; le lingot d'or fait déborder la cuve pleine; la grande cuve récupère l'eau dont la quantité est représentative du volume du lingot.

- La cuve est à nouveau remplie à ras-bord, et elle est placée dans une deuxième grande cuve vide; la couronne fait déborder la cuve pleine; la deuxième grande cuve récupère l'eau dont la quantité est représentative du volume de la couronne. - Il suffit de comparer le volume dans chacune des deux grandes cuves. L'orfèvre est confondu! Le volume dans la cuve-couronne est légèrement plus grand; il y a bien eu remplacement d'or par de l'argent. Variante: On opère la première phase de l'expérience: le lingot d'or déplace une certaine quantité d'eau. Ensuite, on remplace le lingot par la couronne. Si la couronne est en or pur, l'eau ne débordera pas. Par contre, si sa densité de la couronne est plus faible (son volume est plus important pour la même masse), de l'eau supplémentaire débordera.

Légende?

L'histoire ajoute qu'Archimède aurait été mis à mort s'il n'avait pas pu démontrer la fraude.

C'est l'architecte romain Vitruve qui raconte cette histoire quasiment deux siècles après les faits.

Mais, il semble que ce soit plutôt une légende.

En effet, la différence de volume aurait dû être si faible qu'Archimède, avec les appareils de l'époque n'aurait pas pu mesurer l'écart.

Calcul:

Couronne or	P = 1000 g V = 1000 / 19,5 = 51,28 cm^3
Couronne or-argent	P = 700g or + 300 g argent V = 700 / 19,5 + 300 / 10,5 = 64,46 cm^3
Différence	64,46 – 51,28 = 13,18 cm^3
Couronne Récipient	D = 18 cm (exemple) D = 20 cm
Hauteur d'eau

Une différence de 0,4 mm n'est pas discernable avec une telle expérience, surtout à cette époque-là. Ne serait-ce que du fait de la tension superficielle.

Expérience basée

sur le théorème d'Archimède

Comment réaliser une expérience prouvant la fraude en utilisant strictement le principe d'Archimède, c'est-à-dire en mesurant une poussée due à un fluide? L'expérience se passe également en deux temps: à sec et en milieu aqueux.

La pesée est effectuée en équilibrant le poids de la couronne par une quantité suffisante d'or.

Les deux objets sont immergés complètement dans de l'eau.
On note P_air le poids dans l'air et P_eau celui dans l'eau.
P_A est la poussée d'Archimède, celle qui allège le poids.

La couronne n'est pas en or pur. Elle comporte de l'argent moins dense que l'or. À poids égal, l'argent occupe plus de place. Le volume de la couronne or-argent est plus grand que celui des lingots d'or.

La poussée d'Archimède, force verticale dirigée vers le haut, est plus grande pour la couronne du fait qu'elle occupe plus de volume. La couronne est donc allégée par rapport aux lingots d'or.

Le fléau de la balance bascule vers la gauche. Du côté de l'or pur, plus lourd dans l'eau que la couronne. Preuve de la supercherie.

Calcul:

Couronne or	P = 1000 g V = 1000 / 19,5 = 51,28 cm^3 PE = 1000 – 51,28 = 948,72 g
Couronne or-argent	P = 700g or + 300 g argent V = 700 / 19,5 + 300 / 10,5 = 64,46 cm^3 PE = 1000 – 64,46 = 935,53 g
Différence de poids dans l'eau	948,72 – 935,53 = 13,18 g

Une différence de 13 grammes est appréciable même une balance du temps d'Archimède.

Voir Énigmes de pesées

Merci à Baptiste Fertille pour sa lecture attentive

Retour	Théorème d'Archimède – Débutants Théorème d'Archimède – Développements
Voir	Archimède – Biographie Archimède et ses contemporains Histoire Levier Pompage, paille, girafe … Projectile
Aussi	Dicomot Masse et poids Pesanteur Force
Site	Poussée d'Archimède – Wikipédia Principe d'Archimède – Animation Principe d'Archimède – Imago Mundi The Golden Crown – Archimedes Pages – Math.nyu.edu
Cette page	http://villemin.gerard.free.fr/aScience/Physique/EurekaCo.htm