NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/01/2012 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Électronique
Débutants Général	BASES			Glossaire Général
INDEX Électronique	Loi d'Ohm	Résistances	Résistance interne
	Exemple	Réseaux	Théorèmes
	Sommaire de cette page >>> Modélisation d'un réseau >>> Multi-sources

Simplification des circuits

Théorème de Thévenin

Théorème de superposition

Deux théorèmes utiles pour calculer des circuits complexes.

Modélisation d'un réseau

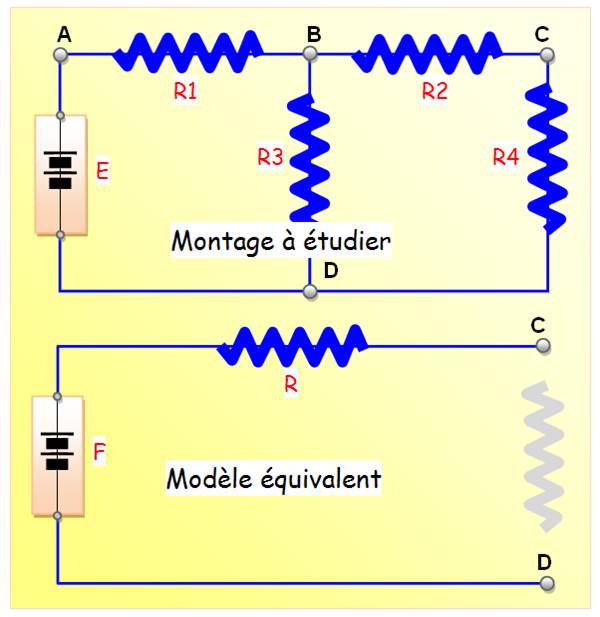
On sait calculer les tensions sur un pont diviseur et sur des réseaux plus complexes. Une méthode d'approche consiste à réduire la complexité en remplaçant une partie du circuit par son modèle équivalent. C'est l'objet du théorème de Thévenin. Exemple de montage Il s'agit de déterminer la valeur de la f.e.m équivalente F et de la résistance équivalente R. La résistance R4 est considérée comme une charge non connectée.

Calcul de F Il n'y a pas de courant dans la résistance R2. Alors UBD = UCD. Les résistances R1 et R2 constitue un pont diviseur: UBD = E . R3 / (R1 + R3) Dans le modèle, il n'y a pas de charge; le courant est nul et tension aux bornes de C et D est égale à F.

E = 10 V (en bleu: données) R1 = 1 kΩ R3 = 3 kΩ UBD = UCD = 10 x 3/4 = 7, 5 V F = 7, 5 V

Calcul de R Selon le théorème de Thévenin: la résistance R du modèle équivalent correspond à la résistance entre les bornes du montage sans charge en ayant pris soin d'éliminer les générateurs tout en conservant leur résistance interne. En conséquence: R1 et R3 sont en parallèle, le tout en sérié avec R2: R = R2 + (R1 . R3) / (R1 + R3)

R2 = 0,5 kΩ R = 0,5 + 3/4 = 1,25 k

Calcul de U aux bornes de R4 À nouveau le coup du pont diviseur: UCD = F . R4 / (R + R4)

R4 = 0,75 k UCD = 7, 5 x 0,75 / 2 = 2,8 V

Multi-sources
Lorsque plusieurs sources électriques sont présentes, comment s'y prendre? Le théorème de superposition simplifie le problème en le partageant en autant de circuit que de sources. Pour faire le bilan, il suffit d'ajouter les résultats. Le montage illustre ce cas et montre les deux montages ne contenant qu'un seul générateur. L'autre est retiré, sauf sa résistance interne.

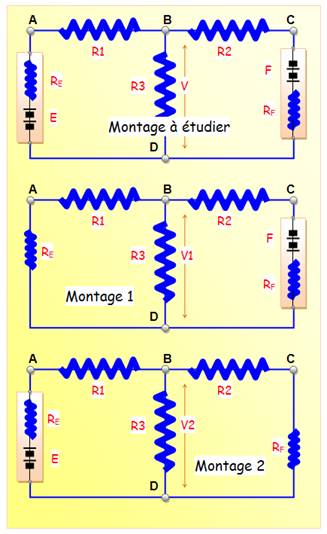
Montage 1 Entre B et D, résistances en série (unité: kilo ohms) R2F = 2 + 1 = 3 R1E = 2 + 1 = 3 Entre B et D, résistances en parallèle R13E = 3 x 5 / (3 + 5) = 1,875 Pont diviseur V1 = F . R13F / (R13F + R2F) = 10 x 1,875 / (1,875 + 3) = 3,84 V

F = 10 V (en bleu: données) R1 = 2 kΩ R2 = 2 kΩ R3 = 5 kΩ RE = 1 kΩ RF = 1 kΩ La contribution du générateur F à la tension V aux bornes de B et D vaut 3, 84 volts

Montage 2 On retrouve R2F = 2 + 1 = 3 R1E = 2 + 1 = 3 Entre B et D, résistances en parallèle R23F = 3 x 5 / (3 + 5) = 1,875 Pont diviseur V2 = E . R23F / (R23F + R1E) = 20 x 1,875 / (1,875 + 3) = 7,69 V

E = 20 V La contribution du générateur F à la tension V aux bornes de B et D vaut 7, 69 volts

Bilan On observe que les générateurs E et F sont montés l'un dans un sens et l'autre dans l'autre sens. Les contributions se retranchent: V = V2 – V1 Note: Le signe final n'a pas d'importance. Si on a orienté dans un sens et que le signe est négatif, il suffit d'inverser ce sens.

La contribution des générateurs E et F à la tension V aux bornes de B et D vaut: 7, 69 – 3, 84 = 3 ,85 volts

Suite	Le tube diode Loi d'Ohm
Voir	Sciences – Index
Livres	Électronique pratique – J.-M. Fouchet et A. Perez-Mas – Dunod – 1999 - Un très grand classique, très pédagogique Théorie et pratique de la radioélectricité – Lucien Chrétien – Chiron – 1960 – C'est avec ce livre que j'ai fait mes premiers pas en électronique.
Cette page	http://villemin.gerard.free.fr/aScience/Electron/Theoreme.htm