|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
F |
Nombre / Diviseurs
/ Additifs /
DÉFICIENT Abondants / P |
||
|
Approche |
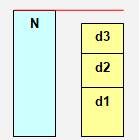
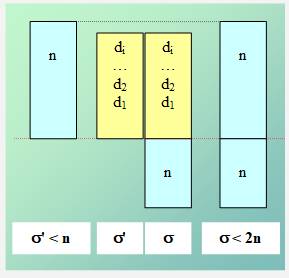
Un nombre entier n peut être divisé p Si leur somme est inférieure au nombre n,
ce nombre est déficient. |
|
|
|
Exemples |
Nombre |
Diviseurs 1, 2, 4 1, 3, 7 |
Somme 7
< 8 11 < 21 |
|
Définitions |
Un nombre est déficient Formul Le nombre n est abondant Le nombre n est abondant Déficience de n La déficience de n est la différence |
|
|
Propriétés |
Les nombres 1, 2, 3 jusqu'à 19 sont déficients (hors 6, parfait
et les multiples de 6, abondants). La plage de nombres abondants consécutifs
ne peut pas dépasser 5, car tous les nombres multiples de 6 sont abondants. Il existe une infinité de nombres
déficients. Pour N jusqu'à 100 compris, il y a: 76 nombres déficients; 22 abondants (le nombre 100 étant lui-même
abondant); et 2
nombres parfaits (6 et 28). Tous les nombres premiers et leurs
puissances sont déficients. Exemple 11, somme des diviseurs propres = 1 et 1 < 11 Tous les nombres produits de deux nombres
premiers différents sont déficients Exemple 3 x 5 = 15, somme des diviseurs = 1 + 3 + 5 = 9 et 9 < 15 Tous les diviseurs d'un nombre déficient ou
d'un nombre parfait sont déficients. |
|
Angl |
An deficient number or defective number is
a number n |
![]()
Nombre
déficient le plus petit selon l'unité du nombre
Avec,
en dessous, la somme de ses diviseurs propres
(Hors
nombres premiers qui sont tous déficients)
|
10 8 |
1 0 |
22 14 |
33 15 |
4 3 |
15 9 |
16 15 |
27 13 |
8 7 |
9 4 |
|
|
|
|
Liste des 751 nombres déficients jusqu'à 1000 Ce sont les nombres qui ne sont pas abondants (246), ni parfait (3, avec 6, 28 et 496) Total 751
+ 246 + 3 =1000 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13,
14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38,
39, 41, 43, 44, 45, 46, 47, 49, 50, 51, 52, 53, 55, 57, 58, 59, 61, 62, 63,
64, 65, 67, 68, 69, 71, 73, 74, 75, 76, 77, 79, 81, 82, 83, 85, 86, 87, 89,
91, 92, 93, 94, 95, 97, 98, 99, 101, 103, 105, 106, 107, 109, 110, 111, 113,
115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 127, 128, 129, 130, 131,
133, 134, 135, 136, 137, 139, 141, 142, 143, 145, 146, 147, 148, 149, 151,
152, 153, 154, 155, 157, 158, 159, 161, 163, 164, 165, 166, 167, 169, 170,
171, 172, 173, 175, 177, 178, 179, 181, 182, 183, 184, 185, 187, 188, 189,
190, 191, 193, 194, 195, 197, 199, 201, 202, 203, 205, 206, 207, 209, 211,
212, 213, 214, 215, 217, 218, 219, 221, 223, 225, 226, 227, 229, 230, 231,
232, 233, 235, 236, 237, 238, 239, 241, 242, 243, 244, 245, 247, 248, 249,
250, 251, 253, 254, 255, 256, 257, 259, 261, 262, 263, 265, 266, 267, 268,
269, 271, 273, 274, 275, 277, 278, 279, 281, 283, 284, 285, 286, 287, 289,
290, 291, 292, 293, 295, 296, 297, 298, 299, 301, 302, 303, 305, 307, 309,
310, 311, 313, 314, 315, 316, 317, 319, 321, 322, 323, 325, 326, 327, 328,
329, 331, 332, 333, 334, 335, 337, 338, 339, 341, 343, 344, 345, 346, 347,
349, 351, 353, 355, 356, 357, 358, 359, 361, 362, 363, 365, 367, 369, 370,
371, 373, 374, 375, 376, 377, 379, 381, 382, 383, 385, 386, 387, 388, 389,
391, 393, 394, 395, 397, 398, 399, 401, 403, 404, 405, 406, 407, 409, 410,
411, 412, 413, 415, 417, 418, 419, 421, 422, 423, 424, 425, 427, 428, 429,
430, 431, 433, 434, 435, 436, 437, 439, 441, 442, 443, 445, 446, 447, 449,
451, 452, 453, 454, 455, 457, 458, 459, 461, 463, 465, 466, 467, 469, 470,
471, 472, 473, 475, 477, 478, 479, 481, 482, 483, 484, 485, 487, 488, 489,
491, 493, 494, 495, 497, 499, 501, 502, 503, 505, 506, 507, 508, 509, 511,
512, 513, 514, 515, 517, 518, 519, 521, 523, 524, 525, 526, 527, 529, 530,
531, 533, 535, 536, 537, 538, 539, 541, 542, 543, 545, 547, 548, 549, 551,
553, 554, 555, 556, 557, 559, 561, 562, 563, 565, 566, 567, 568, 569, 571,
573, 574, 575, 577, 578, 579, 581, 583, 584, 585, 586, 587, 589, 590, 591,
592, 593, 595, 596, 597, 598, 599, 601, 602, 603, 604, 605, 607, 609, 610,
611, 613, 614, 615, 617, 619, 621, 622, 623, 625, 626, 627, 628, 629, 631,
632, 633, 634, 635, 637, 638, 639, 641, 643, 645, 646, 647, 649, 651, 652,
653, 655, 656, 657, 658, 659, 661, 662, 663, 664, 665, 667, 668, 669, 670,
671, 673, 674, 675, 676, 677, 679, 681, 682, 683, 685, 686, 687, 688, 689,
691, 692, 693, 694, 695, 697, 698, 699, 701, 703, 705, 706, 707, 709, 710,
711, 712, 713, 715, 716, 717, 718, 719, 721, 722, 723, 724, 725, 727, 729,
730, 731, 733, 734, 735, 737, 739, 741, 742, 743, 745, 746, 747, 749, 751, 752,
753, 754, 755, 757, 758, 759, 761, 763, 764, 765, 766, 767, 769, 771, 772,
773, 775, 776, 777, 778, 779, 781, 782, 783, 785, 787, 788, 789, 790, 791,
793, 794, 795, 796, 797, 799, 801, 802, 803, 805, 806, 807, 808, 809, 811,
813, 814, 815, 817, 818, 819, 821, 823, 824, 825, 826, 827, 829, 830, 831,
833, 835, 837, 838, 839, 841, 842, 843, 844, 845, 847, 848, 849, 850, 851,
853, 854, 855, 856, 857, 859, 861, 862, 863, 865, 866, 867, 869, 871, 872,
873, 874, 875, 877, 878, 879, 881, 883, 884, 885, 886, 887, 889, 890, 891,
892, 893, 895, 897, 898, 899, 901, 902, 903, 904, 905, 907, 908, 909, 911,
913, 914, 915, 916, 917, 919, 921, 922, 923, 925, 926, 927, 929, 931, 932,
933, 934, 935, 937, 938, 939, 941, 943, 944, 946, 947, 949, 950, 951, 953,
955, 956, 957, 958, 959, 961, 962, 963, 964, 965, 967, 969, 970, 971, 973,
974, 975, 976, 977, 979, 981, 982, 983, 985, 986, 987, 988, 989, 991, 993,
994, 995, 997, 998, 999 |
|
Voir Programmtion
![]()
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()