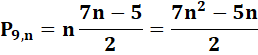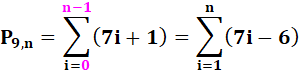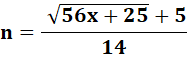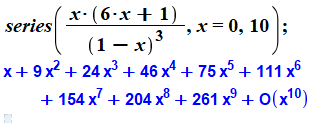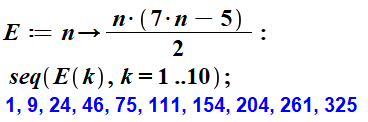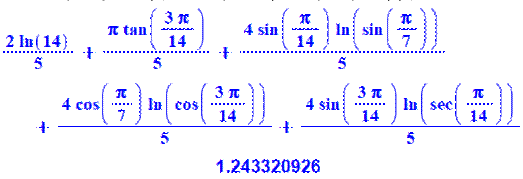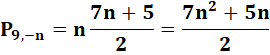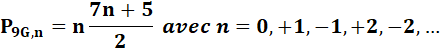|
Édition du: 19/06/2020 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
NOMBRES ENNÉAGONAUX Nonagonaux 9-gonal Nombres
construits en déposant des points sur des ennéagones
gigognes, chacun appuyé sur le précédent. |
||
|
|
Sommaire de cette page >>>
Nombres ennéagonaux >>>
Nombres ennéagonaux – Tables >>>
Propriétés avec les nombres entiers >>>
Propriétés avec les nombres triangulaires >>>
Nombres ennéagonaux généralisés >>>
Langues |
Débutants Nombres
figurés ou
géométriques Glossaire |
|
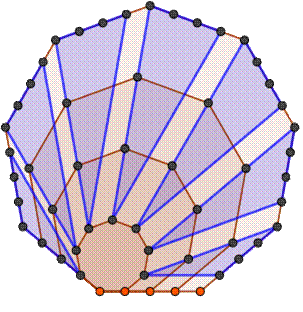
Construction des nombres
ennéagonaux
La quantité "en plus" est appelée: gnomon |
|
||||||||||||||||||||||||||
|
Notation et formules La formule en somme
résulte du décompte vu ci-dessus. L'incrément étant égal à: |
|
||||||||||||||||||||||||||
|
Caractérisation Sorte de racine ennéagonale. |
Si
n est un nombre entier alors x est le énième nombre ennéagonal. Sinon, il
n'est pas ennéagonal. N
est une des racines de x = 1/2 (7n² – 5n). |
||||||||||||||||||||||||||
|
Fonction génératrice L'instruction demande le développement sur dix
termes. |
|
||||||||||||||||||||||||||
|
Programme |
|
||||||||||||||||||||||||||
|
Somme des inverses Constante calculée pour n jusqu'à 10 000: |
|
||||||||||||||||||||||||||
|
Les 100 premiers ennéagonaux |
1, 9, 24, 46, 75, 111, 154, 204, 261, 325, 396, 474, 559,
651, 750, 856, 969, 1089, 1216, 1350, 1491, 1639, 1794, 1956, 2125, 2301,
2484, 2674, 2871, 3075, 3286, 3504, 3729, 3961, 4200, 4446, 4699, 4959, 5226,
5500, 5781, 6069, 6364, 6666, 6975, 7291, 7614, 7944, 8281, 8625, 8976, 9334,
9699, 10071, 10450, 10836, 11229, 11629, 12036, 12450, 12871, 13299, 13734,
14176, 14625, 15081, 15544, 16014, 16491, 16975, 17466, 17964, 18469, 18981,
19500, 20026, 20559, 21099, 21646, 22200, 22761, 23329, 23904, 24486, 25075,
25671, 26274, 26884, 27501, 28125, 28756, 29394, 30039, 30691, 31350, 32016,
32689, 33369, 34056, 34750 |
|
|
Ennéagonaux carrés |
1, 9,
1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, … |
|
|
Parité |
Cycle:
impair-Impair- pair-pair. |
|
|
P9,n = 7Tn-1 + n (Illustration) = 7/2 (n – 1)n + n = 1/2 (7n² – 7n + 2n) = 1/2 (7n² – 5n) |
|
|
|
Ennéagonaux du deuxième ordre |
Même
formule que pour les ordinaires avec signe plus. |
|
|
Les premiers ennéagonaux du 2e
ordre |
6, 19, 39, 66, 100, 141, 189, 244, 306, 375, 451,
534, 624, 721, 825, 936, 1054, 1179, 1311, 1450, … |
|
|
Ennéagonaux généralisés |
Soit la réunion des nombres ennéagonaux
ordinaires avec les centrés. |
|
|
Les premiers ennéagonaux
généralisés (ordinaires et du 2e ordre) |
1, 6, 9, 19, 24, 39, 46, 66, 75, 100, 111, 141, 154, 189,
204, 244, 261, 306, 325, 375, 396, 451, 474, 534, 559, 624, 651, 721, 750,
825, 856, 936, 969, 1054, 1089, 1179, 1216, 1311, 1350, 1450, 1491, 1596,
1639, 1749, 1794, 1909, 1956, 2076, … |
|
|
Anglais: A nonagonal number is a figurate number. Allemand:
Nonagonalzahl oder Neuneckszahl Espagnol: Un número
nonagonal es un número figurado. Italien: Un numero
ennagonale è un numero poligonale |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |