|
Édition du: 27/04/2025 |
|
INDEX |
Pesées – Partitions |
||
![]()
|
Pesées avec des poids de 4kg et 7kg Est-il possible
de faire toutes les pesées possibles avec de tels poids? Ou de manière équivalente
est-il possibles de faire n'importe quelle somme avec des pièces de 4 euros
et de 7 euros? Plus
généralement: partition des nombres avec des 4 et des 7. |
||
|
|
Sommaire de cette page >>> Partition en 4 et 7 >>> Démonstration |
Débutants Glossaire |
|
Comment
partitionner 4, 9 et 13 à la fois avec les nombres de 1 à 7 utilisé ou pas
mais une seule fois seulement ? |
|
|
||
|
Démontrez la proposition
suivante: Il est possible
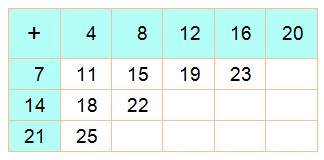
de partitionner tous les nombres au-delà de 18 avec seulement des 4 et de 7. La table d'addition
ci-contre montre la pertinence du démarrage à n = 18. |
Additions en 4 et 7
Sont présents: 4, 7, 8, 11, 12, 14, 15, 18, 19, 20 21,
22, 23, 24, 25 … |
|
|
Donc de 18 à 21, la
proposition est vraie. |
|
|
|
Supposons la vraie pour ces
valeurs et au-delà, jusqu'à k. |
P(k) vraie pour tous j de 18
à k avec k |
|
|
Il faut montrer que sous cette
supposition, la proposition est toujours vraie pour k + 1 |
Or la proposition est vraie pour k – 3 puisque |
|
|
Or, selon notre supposition: |
k k – 3 |
|
|
En ajoutant simplement un 4 de plus, la proposition
reste vraie: |
k – 3 + 4 k +1 |
|
|
La proposition est vraie de
18 à 21 or si on suppose qu'elle est vraie au-delà, jusqu'à un certain point,
elle reste vraie pour le point suivant. |
Par induction,
la proposition est vraie pour tous les entiers supérieurs à18. |
|
|
Énigme Comment
partitionner 4, 9 et 13 à la fois avec les nombres de 1 à 7 utilisé ou pas
mais une seule fois seulement ? Observations La
somme des nombres de 1 à 7 vaut ½ 7 x
8 = 28 et celle des nombres à partitionner est 4 + 9 + 13 = 26. Le nombre 2
ne peut pas être utilisé. Le
nombre 13 ne peut être atteint que par la somme 6 + 7 = 13. Solution 13
= 6 + 7; 9 = 5 + 4 et 4 = 1 + 3 D'après un jeu
mathématique d'Hervé Lehning – Futura Science |
Retour
/ Jeux et énigmes – Index
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()