|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Énigmes: trouver un nombre Avec indications sur les diviseurs Problèmes dont l'énoncé est
si succinct et sibyllin que sa résolution semble impossible. Cas simples avant d'aborder le problème plus ardu de Freudenthal. |
|
|
||
|
Énoncé Soit un
nombre entier entre 1 et 12. Sachant
que la somme des diviseurs est 12, dire quel est ce nombre. C'est impossible,
ils sont deux: 6 et 11. En
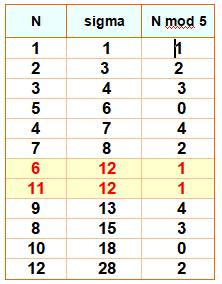
revanche, on peut sûrement dire que le reste de leur division par 5 est 1. Explication Le tableau montre que, parmi les nombres de 1 à
12, il existe deux nombres, et deux nombres suelement, ayant la même somme
des diviseurs (sigma). Le reste de leur division par 5 (n mod 5)
est bien 1, dans les deux cas. |
Nombres selon la somme des
diviseurs
Seuls les
nombres 6 et 11 ont une somme de diviseurs égale à 12. L'énoncé
aurait pu proposer les nombres de 1 à 100 ou plus, mais l'énigme aurait été
plus difficile à résoudre. |
|
|
|
||
|
Énoncé On
choisit un nombre entier N compris entre 1 et 12. On
indique la somme des diviseurs à l'un
et le plus grand diviseur premier
de N à l'autre. Chacun
répond qu'il ne peut pas dire quel est N. Un tiers
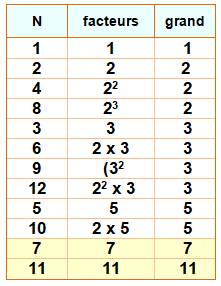
présent sait deviner la valeur de N. Explication Avec la première réponse, comme pour l'énigme
précédente, on déduit que N = {6, 11}. Avec la seconde, et avec le même principe, on
déduit que N = {1, 2, …, 10}. En effet, s'il n'y avait qu'une solution, il
aurait répondu 7 ou 11. Il est en présence de plusieurs réponses, donc un
nombre parmi 1 à 10. En recoupant les deux informations: c'est 6 ou
11, mais ce n'est pas 11, alors c'est 6. |
Nombres selon le plus grand
diviseur
|
|
|
|
||
|
Énoncé On
choisit un nombre entre 1 et 20 On
indique la somme des diviseurs à l'un et le plus grand diviseur à l'autre. Le
premier dit qu'il ne sait pas. Ensuite, l'autre dit qu'il ne sait pas non
plus. Donner la
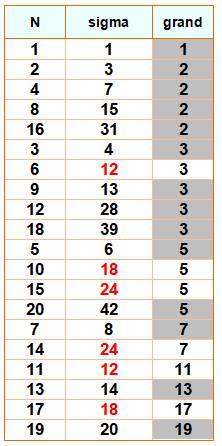
quantité de diviseurs de N Explication Avec la première réponse, on déduit que N = {6, 11} ou {10, 17} ou {14, 15}. Dans la liste des nombres, on ne retient que
ceux-là et on indique le facteur le plus grand. Avec la seconde réponse disant qu'il y a indétermination,
on en déduit que les nombres à retenir sont 10 et 15. Or, les diviseurs de 10 sont {1, 2, 5, 10}, soit
4 diviseurs. Et, les diviseurs de 15 sont {1, 3, 5, 15}, soit
4 diviseurs. Réponse à la question posée: quatre diviseurs. |
Nombres selon le plus grand
diviseur
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Livre |
|
|
Cette page |
![]()