passerelle sur bassin

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/09/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	Longueurs et aires			Glossaire Géométrie
INDEX Géométrie Jeux et énigmes	Dissection	Carré	Bassin	Sapin de Noël
	Chèvre et carré	Chèvre et cercle	Puits
		Sommaire de cette page >>> Problème >>> Solution

Traversée d'un plan d'eau

avec des planches

Château et douves / Île et pont / Rivière et planche

Avec une planche solide posée sur les deux berges, je franchis la rivière. Même chose pour un bassin pour rejoindre le terre-plein central.

Un problème amusant consiste à voir si je peux minimiser la longueur des planches. Oui, je peux, avec une solution astucieuse, mais la longueur ne diminue pas autant qu'on le pense.

Anglais a castle is surrounded by a 5 meters wide, rectangular moat.

Can you cross using nothing except two planks that are 4,8 meters long.

Problème

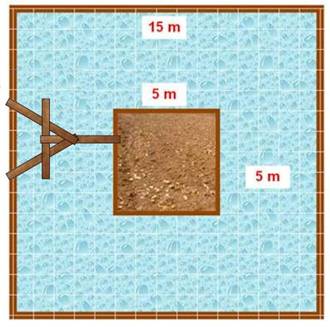
Problème 1

Imaginez un carré central de 5 m de côté au milieu d'un bassin d'eau lui-même un carré de 15 m de côté. Je souhaite passer au centre sans me mouiller. Je dispose d'une planche (madrier). Quelle est sa longueur minimale?

Solution 1

Je place ma planche d'un bord à l'autre: soit 5m de long, ou un plus, de quoi la poser sur les bords.
Solution facile!

Problème 2

Hélas, je ne dispose pas de planche de 5m de long.

Mais quelle est la longueur minimale requise avec deux planches utilisées astucieusement?

Voir Solution / Brève 53-1050

Solutions
Idée géniale! Avec deux planches plus courtes que les 5 m nécessaires pour un passage direct, j'établis un passage. Mais quelle est la longueur minimale de ces deux planches? J'appelle x la longueur à partir du coin du bassin jusqu'au point de dépose de la planche en biais. Note: on néglige toujours la largeur de la planche. Le calcul serait un peu plus compliqué mais ne changerait pas fondamentalement le résultat théorique.
Longueur de la planche en travers:
Longueur de l'autre planche = diagonale du grand carré – ½ diagonale du petit carré:
Pour x = 0, soit une seule planche (D):
Pour x = 10, soit une seule planche (d):
En passant de x= 0 à x = 10, Une des longueurs croit lorsque l'autre décroit. Elles ont même longueur pour:
Longueur des planches:
On constate que malgré tout la planche doit être proche des 5 mètres ! La réduction de la longueur n'est que de 6%.
Par exemple, pour une distance de 1 mètre, à la place des 5 m, les deux planches devront mesurer:	100 cm – 6% de 100 cm = 100 – 6 = 94 cm