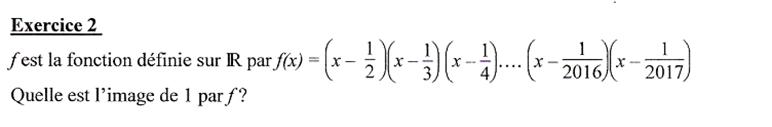|
|||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du DEUXIÈME DEGRÉ Initiation Exemple d'approche des
fonctions et équations du deuxième degré. |
|
|
|
|
Voir Carré en
géométrie Rappel
de la définition
Voir DicoMot Maths 1) Ensembles
de définition des fonctions Le périmètre est
une longueur qui s'exprime avec une quantité de
mètres, c'est un nombre réel (nombre avec éventuellement des décimales, donc
pas un nombre entier): Ensemble de définition du périmètre: L'aire est un
produit de deux longueurs qui s'expriment
chacune avec un nombre réel: Ensemble de définition de l'aire: 2) Expressions de A(x) et P(x) La figure montre
bien que le carré initial est "dilaté" de la même quantité sur deux
côtés adjacents. La nouvelle figure reste encore un carré de côté 6 + x. Si x vaut 4 cm, par exemple, les quatre côtés
mesureront: 6 + 4 = 10 cm. Aire du carré
= longueur du côté au carré: A(x) = (6 + x)² = x² + 12x + 36 (On verra qu'il est
inutile de développer) Périmètre du
carré = 4 fois la longueur du côté: P(x)
= 4(6 + x) = 4x + 24 3) Valeur
de P(x) si A(x) = 51,84 A(x) = (6 + x)² = 51,84
= 7,2² 6 + x = 7,2 P(x) = 4(6 + x) = 4 . 7,2 = 28,8 cm (le point et non x
pour éviter
la confusion avec l'inconnue x) 4) Valeur
de A(x) si P(x) = 32,80 P(x) = 4(6 + x) = 32,80 6 + x = 8,20 A(x) = (6 + x)² = 8,20² = 67,24 cm² |
|
|
|
|
|
Rappel: la fonction
est définie sur La question
demande quelle est l'image (on pourrait dire
plus simplement: la valeur) de f(x) pour x =
1. L'image de
1 par f veut donc dire: si je prends x = 1, comment ce 1 se
transforme-t-il en l'injectant dans la "moulinette" de la fonction
f ?
Valeur de f(x =
1)
On reformule
f(x=1) en calculant les fractions
dans les parenthèses. Exemple:
Soit pour f(x =
1):
On remarque que
le numérateur de l'une est égal au dénominateur de la précédente.Ce qui
occasionne une simplification massive:
|
|
|
|
|
|
Avec 20 mètres de
grillage, cette personne peut entourer un potager de 20 m de périmètre quelle
que soit sa forme. S'il est rectangulaire,
ce périmètre vaut (a sa longueur et b
sa largeur): P = 2(a + b) = 20
=> a + b = 10 et b = 10 – a Son aire: A = a.b = 20,16 En remplaçant b
par sa valeur en fonction de a: A = a.(10 – a) = 10a – a² = 20,16 Soit une
expression du deuxième degré (car existence de a²) égale à 0; ce qui
s'appelle une équation du deuxième degré: a² – 10a + 20,16
= 0 Sauf cas très
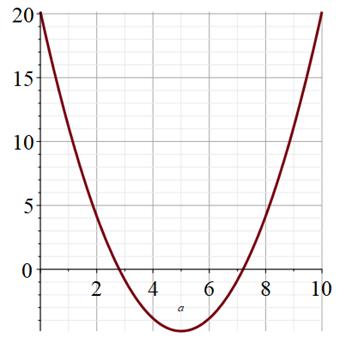
particulier, il n'y a pas de solution évidente pour résoudre cette équation. Nous avons néanmoins trois possibilités. a) Résolution
graphique
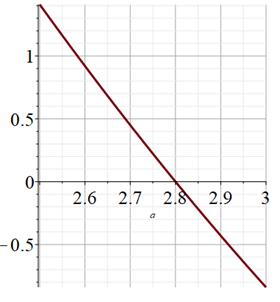
Deux coupures de
l'axe des x en 2,8 et 7,2. C'est bien ce que nous cherchons, car c'est lorsque la
courbe coupe l'axe des abscisses que la fonction f vaut 0. Confirmation en
zoomant:
Solutions:
a = 2,8 et b = 10 – 2,8 = 7,2 ou a = 7,2 et b = 10 – 7,2 = 2,8 L'usage veut que
a, la longueur soit plus grande que b, la largeur. On conservera: a = 7,2 cm et b
= 2,8 cm Vérification P = 2 (7,2 + 2,8) = 20 cm A = 7,2 . 2,8 = 20,16 cm² b) Résolution
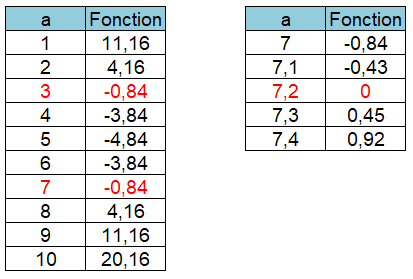
par tableau de valeurs (c'est-à-dire par encadrement de la solution) Un premier
passage avec les valeurs de 1 à 10
montre deux solutions aux alentours de 3 et 7. Un second passage
autour de 7 (par exemple), en progressant par pas de 0,1 donne directement
une des solutions (7,2)
c) Résolution
de l'équation Sans
doute pas encore étudié en cours. Donc pour information et pour montrer que
l'on peut trouver les solutions par l'algèbre. Voir Résolution
générale des équation du deuxième degré Équation à
résoudre: a² – 10a + 20,16 = 0 On identifie les
trois coefficients: 1a² – 10a + 20,16 = 0 On calcule un
paramètre d:
Les deux racines
de l'équation sont:
|
|
Voir Équation du deuxième
degré – Somme et produit
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()