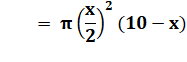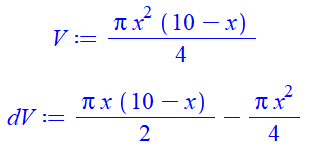|
|||||||||||||||||||||||||||||||||
![]()
|
Fonctions et leurs maximums Exemple simple de résolution
conduisant à la notion de maximum (donc de dérivée,
sans la nommer) sur une fonction. |
|
|
||
|
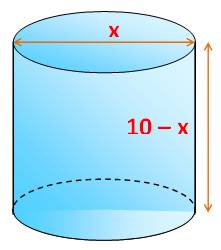
Problème Un
cylindre de diamètre égal à x et de hauteur 10 – x. On se propose
de trouver la valeur de x pour laquelle le cylindre est d'un volume maximum Questions Si V(x) représente le volume du cylindre, quelle
sont les valeurs possible de la variable x. Donner l'expression de V(x). Avec une calculatrice estimer le maximal de V(x).
|
|
|
Voir Fourmi sur
parallélépipède (ou pavé)
|
|
||
|
Intervalle de
valeurs prises par x |
Si le
diamètre est nul (x = 0), la hauteur du disque est égale à 10. (si x se rapproche de 0, on obtient une sorte de
tige) Si la
hauteur est nulle (h = 10 – x), c'est que x vaut 10. (si x tend vers 10, on obtient un disque de
faible épaisseur) Intervalle
de valeurs pour x de 0 à 10. |
|
|
Volume |
|
|
|
|
|||
|
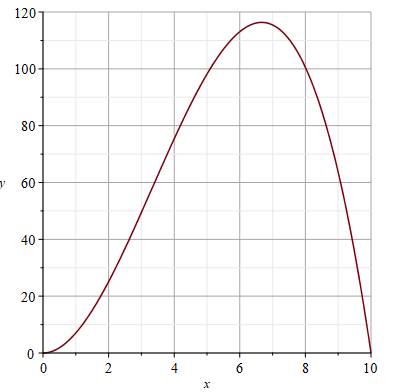
Traçons
la courbe Maximum
pour x autour de 6, 5 et y autour de 115. On
retrouve bien un volume nul pour x = 0 et pour x = 10. |
|
||
|
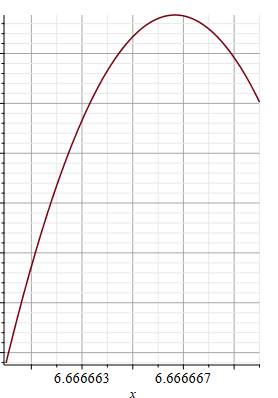
Zoom sur le sommet Calculons: Ce qui constitue le
maximum. Vérification Valeurs pour |
|
||
Recherche systématique avec tableur ou calculatrice
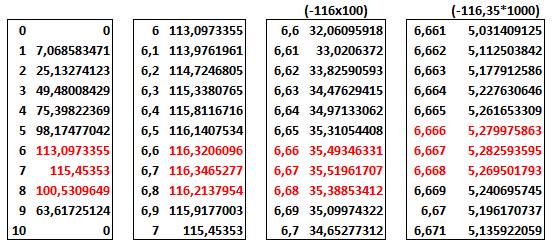
Sur
le 3e tableau, on a retiré 116 et on a multiplié par 100 pour mieux
observer le passage par le minimum.
|
On
a recherché le passage par un maximum "à la main". Nous
apprendrons qu'il existe un outil pour atteindre cet objectif très
précisément, c'est la dérivée.
Et
son passage à 0 est obtenu pour x = 20/3, confirmant la recherche faite
ci-dessus. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()