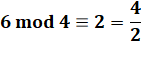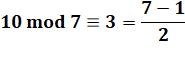|
Édition du: 10/06/2025 |
|
INDEX |
DIVISEURS |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
ANTI-DIVISEURS
Un
concept proche de celui des nombres premiers qui vise justement à étudier la
répartition des nombres premiers, mais en "creux". Les
anti-diviseurs de n sont des nombres particuliers parmi les nombres qui ne
divisent pas n. |
||
|
|
Sommaire de cette page >>> NON-diviseurs >>> ANTI-diviseurs >>> Exemple d'analyse avec le nombre 10 >>> Propriétés >>> Programmes >>> Liste des anti-diviseurs: 2 à 100 >>> Liste des
anti-diviseurs: 100 à 500 >>> Record de quantité d'anti-diviseurs |
Débutants Glossaire |
|
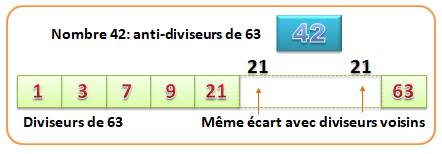
Non-diviseurs On connait les diviseurs. Ce sont tous les
nombres qui divisent un nombre donné. Il s’ensuit logiquement que tout nombre qui n’est
pas un diviseur d’un entier est un non-diviseur. Donc, on dit que les
non-diviseurs de 63 sont tous les entiers inférieurs ou égaux à 63 à
l’exception de 1, 3, 7, 9, 21 et 63. Les anti-viseurs sont définis ci-dessous. |
Div(63) = {1, 3, 7, 9, 21, 63} Non-Div(63) = {2,
4, 5, 6, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30,
31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42,
43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62} Anti-Div(63) =
[2, 5, 6, 14, 18, 25, 42] |
|
|
Non-diviseurs et non-diviseurs
biaisés Certains non-diviseurs sont à égales distance des
deux diviseurs l'entourant. Ceux qui ne le sont pas sont des non-diviseurs
biaisés |
42 est non –biaisé pour 63: 41 est biaisé pour 63: |
|
|
En bref: un nombre k est
anti-diviseur de n en cas d'égalité entre:
|
||
|
Pour les nombres pairs (ADp) Parmi les non-diviseurs pairs,
un anti-diviseur k est tel que: |
Le nombre k = 4 est ADp de n = 6, car |
|
|
Pour les nombres impairs (ADi) Parmi les non-diviseurs impairs,
un anti-diviseur k est tel que: |
Le nombre k = 7 est ADi de n = 10, car |
|
Exemple d'analyse avec le
nombre 10
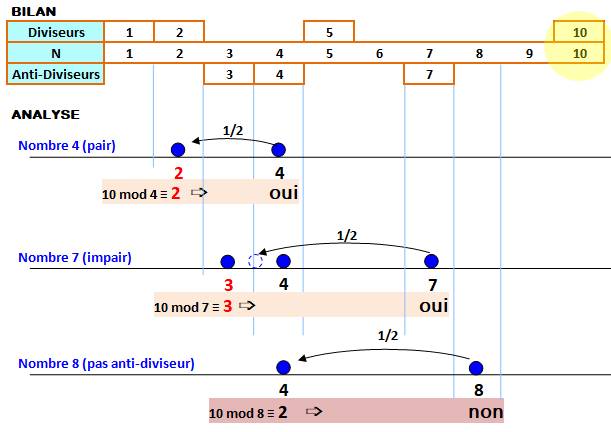
Rappel: 10 mod 4 veut
dire reste de la division de 10 par 4
Voir Brève
63-1246
|
Anti-divisors are the numbers that do not divide a number by
the largest possible margin. E.g. 20 has anti-divisors 3, 8 and 13. An alternative name for anti-divisor is unbiased
non-divisors. |
Les anti-diviseurs sont les nombres qui ne divisent pas un
nombre par la plus grande marge possible. Par exemple, 20 a pour anti-diviseurs 3, 8 et 13. On les appelle aussi non-diviseurs non biaisés. |
|
Tout entier a un le plus
grand anti-diviseur, et c’est à environ 2/3 de n. Ceci peut être utilisé
pour prouver que chaque nombre a un ensemble unique d'anti-diviseurs. Les anti-diviseurs
peuvent être utilisés pour prouver qu’il existe un nombre infini de nombres
premiers. Les anti-diviseurs
harmoniques sont tels que le nombre fois la quantité, divisée par la
somme est un quotient entier. Les anti-premiers
(entiers avec un seul anti-diviseur) sont rares: 3, 4, 6,
96 et 393 216. OEIS
A066466 Nombres anti-parfaits:
ce sont des entiers tels que la somme de ses anti-diviseurs est égal aux
entiers d’origine. Liste: 5, 8, 41, 56, 946, 5 186, 6 874, 8 104, 17 386,
27 024,… OEIS A073930 Nombre anti-amicaux:
la somme des anti-diviseurs de l'un est égale à celle de l'autre. Il existe une formule simple pour trouver des
anti-diviseurs et cette formule peut être utilisée pour obtenir le théorème
selon lequel un entier (2k + 1) est premier ssi k et (k + 1) ne partagent
aucun anti-diviseur. Il est également possible de dériver une méthode
très simple pour générer des nombres premiers. |
|
|
import sympy as sp # Calcul des listes nb=12 nombres = list(range(1, nb+1)) diviseurs_63 = sp.divisors(nb) non_diviseurs = [n for n in nombres\ if n not in diviseurs_63] # Affichage des résultats print(nb,non_diviseurs) |
But Générer
la liste complète des non-diviseurs de 12. Commentaires Création de la liste des
nombres de 1 à 13 Utilisation de l'extension
sympy relative à la théorie des nombres. Création de la liste des
diviseurs de 12. Filtrage pour ne retenir que
les non-diviseurs de 12. Impression du résultat. |
||
|
from sympy.ntheory.factor_ import antidivisors for n in range(1000,1006): print(n,antidivisors(n))
|
But Liste des anti-diviseurs de
1000 à 1005. Utilisation de la commande antidivisor de sympy. Commentaires Appel de sympy Boucle de 1000 à 1006 non
compris. Impression de n et de la
liste de ses anti-diviseurs. |
||
Voir Programmation – Index
|
|
|
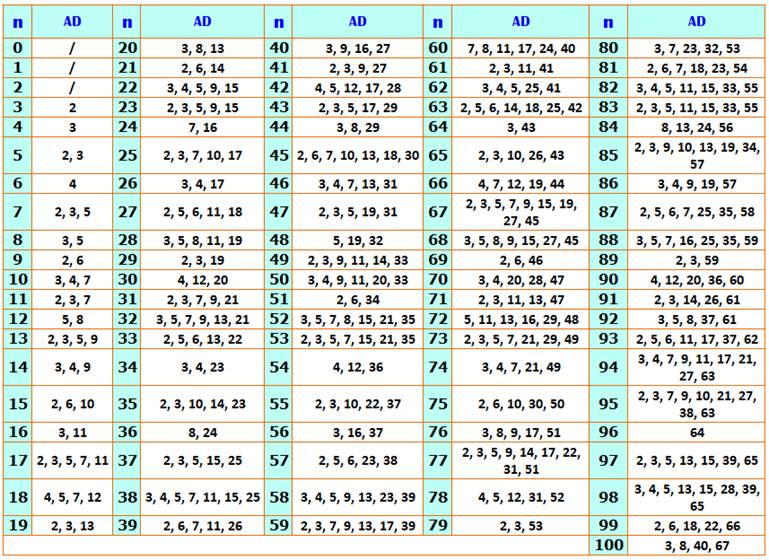
Voir OEIS A066272
- Number of anti-divisors of n.
|
100 [3, 8, 40, 67] 101 [2, 3, 7, 29, 67] 102 [4, 5, 7, 12, 29, 41, 68] 103 [2, 3, 5, 9, 23, 41, 69] 104 [3, 9, 11, 16, 19, 23, 69] 105 [2, 6, 10, 11, 14, 19, 30, 42, 70] 106 [3, 4, 71] 107 [2, 3, 5, 43, 71] 108 [5, 7, 8, 24, 31, 43, 72] 109 [2, 3, 7, 31, 73] 110 [3, 4, 13, 17, 20, 44, 73] 111 [2, 6, 13, 17, 74] 112 [3, 5, 9, 15, 25, 32, 45, 75] 113 [2, 3, 5, 9, 15, 25, 45, 75] 114 [4, 12, 76] 115 [2, 3, 7, 10, 11, 21, 33, 46, 77] 116 [3, 7, 8, 11, 21, 33, 77] 117 [2, 5, 6, 18, 26, 47, 78] 118 [3, 4, 5, 47, 79] 119 [2, 3, 14, 34, 79] 120 [16, 48, 80] 121 [2, 3, 9, 22, 27, 81] 122 [3, 4, 5, 7, 9, 27, 35, 49, 81] 123 [2, 5, 6, 7, 13, 19, 35, 49, 82] 124 [3, 8, 13, 19, 83] 125 [2, 3, 10, 50, 83] 126 [4, 11, 12, 23, 28, 36, 84] 127 [2, 3, 5, 11, 15, 17, 23, 51, 85] 128 [3, 5, 15, 17, 51, 85] 129 [2, 6, 7, 37, 86] 130 [3, 4, 7, 9, 20, 29, 37, 52, 87] 131 [2, 3, 9, 29, 87] 132 [5, 8, 24, 53, 88] 133 [2, 3, 5, 14, 38, 53, 89] 134 [3, 4, 89] 135 [2, 6, 10, 18, 30, 54, 90] 136 [3, 7, 13, 16, 21, 39, 91] 137 [2, 3, 5, 7, 11, 13, 21, 25, 39, 55, 91] 138 [4, 5, 11, 12, 25, 55, 92] 139 [2, 3, 9, 31, 93] 140 [3, 8, 9, 31, 40, 56, 93] 141 [2, 6, 94] 142 [3, 4, 5, 15, 19, 57, 95] 143 [2, 3, 5, 7, 15, 19, 22, 26, 41, 57, 95] 144 [7, 17, 32, 41, 96] 145 [2, 3, 10, 17, 58, 97] 146 [3, 4, 97] 147 [2, 5, 6, 14, 42, 59, 98] 148 [3, 5, 8, 9, 11, 27, 33, 59, 99] 149 [2, 3, 9, 11, 13, 23, 27, 33, 99] 150 [4, 7, 12, 13, 20, 23, 43, 60, 100] |
151 [2, 3, 7, 43, 101] 152 [3, 5, 16, 61, 101] 153 [2, 5, 6, 18, 34, 61, 102] 154 [3, 4, 28, 44, 103] 155 [2, 3, 10, 62, 103] 156 [8, 24, 104] 157 [2, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105] 158 [3, 4, 5, 7, 9, 15, 21, 35, 45, 63, 105] 159 [2, 6, 11, 29, 106] 160 [3, 11, 29, 64, 107] 161 [2, 3, 14, 17, 19, 46, 107] 162 [4, 5, 12, 13, 17, 19, 25, 36, 65, 108] 163 [2, 3, 5, 13, 25, 65, 109] 164 [3, 7, 8, 47, 109] 165 [2, 6, 7, 10, 22, 30, 47, 66, 110] 166 [3, 4, 9, 37, 111] 167 [2, 3, 5, 9, 37, 67, 111] 168 [5, 16, 48, 67, 112] 169 [2, 3, 26, 113] 170 [3, 4, 11, 20, 31, 68, 113] 171 [2, 6, 7, 11, 18, 31, 38, 49, 114] 172 [3, 5, 7, 8, 15, 23, 49, 69, 115] 173 [2, 3, 5, 15, 23, 69, 115] 174 [4, 12, 116] 175 [2, 3, 9, 10, 13, 14, 27, 39, 50, 70, 117] 176 [3, 9, 13, 27, 32, 39, 117] 177 [2, 5, 6, 71, 118] 178 [3, 4, 5, 7, 17, 21, 51, 71, 119] 179 [2, 3, 7, 17, 21, 51, 119] 180 [8, 19, 24, 40, 72, 120] 181 [2, 3, 11, 19, 33, 121] 182 [3, 4, 5, 11, 28, 33, 52, 73, 121] 183 [2, 5, 6, 73, 122] 184 [3, 9, 16, 41, 123] 185 [2, 3, 7, 9, 10, 41, 53, 74, 123] 186 [4, 7, 12, 53, 124] 187 [2, 3, 5, 15, 22, 25, 34, 75, 125] 188 [3, 5, 8, 13, 15, 25, 29, 75, 125] 189 [2, 6, 13, 14, 18, 29, 42, 54, 126] 190 [3, 4, 20, 76, 127] 191 [2, 3, 127] 192 [5, 7, 11, 35, 55, 77, 128] 193 [2, 3, 5, 7, 9, 11, 35, 43, 55, 77, 129] 194 [3, 4, 9, 43, 129] 195 [2, 6, 10, 17, 23, 26, 30, 78, 130] 196 [3, 8, 17, 23, 56, 131] 197 [2, 3, 5, 79, 131] 198 [4, 5, 12, 36, 44, 79, 132] 199 [2, 3, 7, 19, 21, 57, 133] |
|
|
200 [3, 7, 16, 19, 21, 57, 80, 133] 201 [2, 6, 13, 31, 134] 202 [3, 4, 5, 9, 13, 15, 27, 31, 45, 81, 135] 203 [2, 3, 5, 9, 11, 14, 15, 27, 37, 45, 58, 81,
135] 204 [8, 11, 24, 37, 136] 205 [2, 3, 10, 82, 137] 206 [3, 4, 7, 59, 137] 207 [2, 5, 6, 7, 18, 46, 59, 83, 138] 208 [3, 5, 32, 83, 139] 209 [2, 3, 22, 38, 139] 210 [4, 12, 20, 28, 60, 84, 140] 211 [2, 3, 9, 47, 141] 212 [3, 5, 8, 9, 17, 25, 47, 85, 141] 213 [2, 5, 6, 7, 17, 25, 61, 85, 142] 214 [3, 4, 7, 11, 13, 33, 39, 61, 143] 215 [2, 3, 10, 11, 13, 33, 39, 86, 143] 216 [16, 48, 144] 217 [2, 3, 5, 14, 15, 29, 62, 87, 145] 218 [3, 4, 5, 15, 19, 23, 29, 87, 145] 219 [2, 6, 19, 23, 146] 220 [3, 7, 8, 9, 21, 40, 49, 63, 88, 147] 221 [2, 3, 7, 9, 21, 26, 34, 49, 63, 147] 222 [4, 5, 12, 89, 148] 223 [2, 3, 5, 89, 149] 224 [3, 64, 149] 225 [2, 6, 10, 11, 18, 30, 41, 50, 90, 150] 226 [3, 4, 11, 41, 151] 227 [2, 3, 5, 7, 13, 35, 65, 91, 151] 228 [5, 7, 8, 13, 24, 35, 65, 91, 152] 229 [2, 3, 9, 17, 27, 51, 153] 230 [3, 4, 9, 17, 20, 27, 51, 92, 153] 231 [2, 6, 14, 22, 42, 66, 154] 232 [3, 5, 15, 16, 31, 93, 155] 233 [2, 3, 5, 15, 31, 93, 155] 234 [4, 7, 12, 36, 52, 67, 156] 235 [2, 3, 7, 10, 67, 94, 157] 236 [3, 8, 11, 43, 157] 237 [2, 5, 6, 11, 19, 25, 43, 95, 158] 238 [3, 4, 5, 9, 19, 25, 28, 53, 68, 95, 159] 239 [2, 3, 9, 53, 159] 240 [13, 32, 37, 96, 160] 241 [2, 3, 7, 13, 21, 23, 37, 69, 161] 242 [3, 4, 5, 7, 21, 23, 44, 69, 97, 161] 243 [2, 5, 6, 18, 54, 97, 162] 244 [3, 8, 163] 245 [2, 3, 10, 14, 70, 98, 163] 246 [4, 12, 17, 29, 164] 247 [2, 3, 5, 9, 11, 15, 17, 26, 29, 33, 38, 45,
55, 99, 165] 248 [3, 5, 7, 9, 11, 15, 16, 33, 45, 55, 71, 99,
165] 249 [2, 6, 7, 71, 166] 250 [3, 4, 20, 100, 167] 251 [2, 3, 167] 252 [5, 8, 24, 56, 72, 101, 168] 253 [2, 3, 5, 13, 22, 39, 46, 101, 169] 254 [3, 4, 13, 39, 169] 255 [2, 6, 7, 10, 30, 34, 73, 102, 170] 256 [3, 7, 9, 19, 27, 57, 73, 171] 257 [2, 3, 5, 9, 19, 27, 57, 103, 171] 258 [4, 5, 11, 12, 47, 103, 172] 259 [2, 3, 11, 14, 47, 74, 173] 260 [3, 8, 40, 104, 173] 261 [2, 6, 18, 58, 174] 262 [3, 4, 5, 7, 15, 21, 25, 35, 75, 105, 175] 263 [2, 3, 5, 7, 15, 17, 21, 25, 31, 35, 75, 105,
175] 264 [16, 17, 23, 31, 48, 176] 265 [2, 3, 9, 10, 23, 59, 106, 177] 266 [3, 4, 9, 13, 28, 41, 59, 76, 177] 267 [2, 5, 6, 13, 41, 107, 178] 268 [3, 5, 8, 107, 179] 269 [2, 3, 7, 11, 49, 77, 179] 270 [4, 7, 11, 12, 20, 36, 49, 60, 77, 108, 180] 271 [2, 3, 181] 272 [3, 5, 32, 109, 181] 273 [2, 5, 6, 14, 26, 42, 78, 109, 182] 274 [3, 4, 9, 61, 183] 275 [2, 3, 9, 10, 19, 22, 29, 50, 61, 110, 183] 276 [7, 8, 19, 24, 29, 79, 184] 277 [2, 3, 5, 7, 15, 37, 79, 111, 185] 278 [3, 4, 5, 15, 37, 111, 185] 279 [2, 6, 13, 18, 43, 62, 186] 280 [3, 11, 13, 16, 17, 33, 43, 51, 80, 112, 187] 281 [2, 3, 11, 17, 33, 51, 187] 282 [4, 5, 12, 113, 188] 283 [2, 3, 5, 7, 9, 21, 27, 63, 81, 113, 189] 284 [3, 7, 8, 9, 21, 27, 63, 81, 189] 285 [2, 6, 10, 30, 38, 114, 190] 286 [3, 4, 44, 52, 191] 287 [2, 3, 5, 14, 23, 25, 82, 115, 191] 288 [5, 23, 25, 64, 115, 192] 289 [2, 3, 34, 193] 290 [3, 4, 7, 20, 83, 116, 193] 291 [2, 6, 7, 11, 53, 83, 194] 292 [3, 5, 8, 9, 11, 13, 15, 39, 45, 53, 65, 117,
195] 293 [2, 3, 5, 9, 13, 15, 39, 45, 65, 117, 195] 294 [4, 12, 19, 28, 31, 84, 196] 295 [2, 3, 10, 19, 31, 118, 197] 296 [3, 16, 197] 297 [2, 5, 6, 7, 17, 18, 22, 35, 54, 66, 85, 119,
198] 298 [3, 4, 5, 7, 17, 35, 85, 119, 199] 299 [2, 3, 26, 46, 199] 300 [8, 24, 40, 120, 200] 301 [2, 3, 9, 14, 67, 86, 201] 302 [3, 4, 5, 9, 11, 55, 67, 121, 201] 303 [2, 5, 6, 11, 55, 121, 202] 304 [3, 7, 21, 29, 32, 87, 203] 305 [2, 3, 7, 10, 13, 21, 29, 47, 87, 122, 203] 306 [4, 12, 13, 36, 47, 68, 204] 307 [2, 3, 5, 15, 41, 123, 205] 308 [3, 5, 8, 15, 41, 56, 88, 123, 205] 309 [2, 6, 206] 310 [3, 4, 9, 20, 23, 27, 69, 124, 207] 311 [2, 3, 7, 9, 23, 27, 69, 89, 207] 312 [5, 7, 16, 25, 48, 89, 125, 208] 313 [2, 3, 5, 11, 19, 25, 33, 57, 125, 209] 314 [3, 4, 11, 17, 19, 33, 37, 57, 209] 315 [2, 6, 10, 14, 17, 18, 30, 37, 42, 70, 90,
126, 210] 316 [3, 8, 211] 317 [2, 3, 5, 127, 211] 318 [4, 5, 7, 12, 13, 49, 91, 127, 212] 319 [2, 3, 7, 9, 13, 22, 49, 58, 71, 91, 213] 320 [3, 9, 71, 128, 213] 321 [2, 6, 214] 322 [3, 4, 5, 15, 28, 43, 92, 129, 215] 323 [2, 3, 5, 15, 34, 38, 43, 129, 215] 324 [8, 11, 24, 59, 72, 216] 325 [2, 3, 7, 10, 11, 21, 26, 31, 50, 59, 93,
130, 217] 326 [3, 4, 7, 21, 31, 93, 217] 327 [2, 5, 6, 131, 218] 328 [3, 5, 9, 16, 73, 131, 219] 329 [2, 3, 9, 14, 73, 94, 219] 330 [4, 12, 20, 44, 60, 132, 220] 331 [2, 3, 13, 17, 39, 51, 221] 332 [3, 5, 7, 8, 13, 17, 19, 35, 39, 51, 95, 133,
221] 333 [2, 5, 6, 7, 18, 19, 23, 29, 35, 74, 95, 133,
222] 334 [3, 4, 23, 29, 223] 335 [2, 3, 10, 11, 61, 134, 223] 336 [11, 32, 61, 96, 224] 337 [2, 3, 5, 9, 15, 25, 27, 45, 75, 135, 225] 338 [3, 4, 5, 9, 15, 25, 27, 45, 52, 75, 135,
225] 339 [2, 6, 7, 97, 226] 340 [3, 7, 8, 40, 97, 136, 227] 341 [2, 3, 22, 62, 227] 342 [4, 5, 12, 36, 76, 137, 228] 343 [2, 3, 5, 14, 98, 137, 229] 344 [3, 13, 16, 53, 229] 345 [2, 6, 10, 13, 30, 46, 53, 138, 230] 346 [3, 4, 7, 9, 11, 21, 33, 63, 77, 99, 231] 347 [2, 3, 5, 7, 9, 11, 21, 33, 63, 77, 99, 139,
231] 348 [5, 8, 17, 24, 41, 139, 232] 349 [2, 3, 17, 41, 233] |
350 [3, 4, 20, 28, 100, 140, 233] 351 [2, 6, 18, 19, 26, 37, 54, 78, 234] 352 [3, 5, 15, 19, 37, 47, 64, 141, 235] 353 [2, 3, 5, 7, 15, 47, 101, 141, 235] 354 [4, 7, 12, 101, 236] 355 [2, 3, 9, 10, 79, 142, 237] 356 [3, 8, 9, 23, 31, 79, 237] 357 [2, 5, 6, 11, 13, 14, 23, 31, 34, 42, 55, 65,
102, 143, 238] 358 [3, 4, 5, 11, 13, 55, 65, 143, 239] 359 [2, 3, 239] 360 [7, 16, 48, 80, 103, 144, 240] 361 [2, 3, 7, 38, 103, 241] 362 [3, 4, 5, 25, 29, 145, 241] 363 [2, 5, 6, 22, 25, 29, 66, 145, 242] 364 [3, 8, 9, 27, 56, 81, 104, 243] 365 [2, 3, 9, 10, 17, 27, 43, 81, 146, 243] 366 [4, 12, 17, 43, 244] 367 [2, 3, 5, 7, 15, 21, 35, 49, 105, 147, 245] 368 [3, 5, 7, 11, 15, 21, 32, 35, 49, 67, 105,
147, 245] 369 [2, 6, 11, 18, 67, 82, 246] 370 [3, 4, 13, 19, 20, 39, 57, 148, 247] 371 [2, 3, 13, 14, 19, 39, 57, 106, 247] 372 [5, 8, 24, 149, 248] 373 [2, 3, 5, 9, 83, 149, 249] 374 [3, 4, 7, 9, 44, 68, 83, 107, 249] 375 [2, 6, 7, 10, 30, 50, 107, 150, 250] 376 [3, 16, 251] 377 [2, 3, 5, 26, 58, 151, 251] 378 [4, 5, 12, 28, 36, 84, 108, 151, 252] 379 [2, 3, 11, 23, 33, 69, 253] 380 [3, 8, 11, 23, 33, 40, 69, 152, 253] 381 [2, 6, 7, 109, 254] 382 [3, 4, 5, 7, 9, 15, 17, 45, 51, 85, 109, 153,
255] 383 [2, 3, 5, 9, 13, 15, 17, 45, 51, 59, 85, 153,
255] 384 [13, 59, 256] 385 [2, 3, 10, 14, 22, 70, 110, 154, 257] 386 [3, 4, 257] 387 [2, 5, 6, 18, 25, 31, 86, 155, 258] 388 [3, 5, 7, 8, 21, 25, 31, 37, 111, 155, 259] 389 [2, 3, 7, 19, 21, 37, 41, 111, 259] 390 [4, 11, 12, 19, 20, 41, 52, 60, 71, 156, 260] 391 [2, 3, 9, 11, 27, 29, 34, 46, 71, 87, 261] 392 [3, 5, 9, 16, 27, 29, 87, 112, 157, 261] 393 [2, 5, 6, 157, 262] 394 [3, 4, 263] 395 [2, 3, 7, 10, 113, 158, 263] 396 [7, 8, 13, 24, 61, 72, 88, 113, 264] 397 [2, 3, 5, 13, 15, 53, 61, 159, 265] 398 [3, 4, 5, 15, 53, 159, 265] 399 [2, 6, 14, 17, 38, 42, 47, 114, 266] 400 [3, 9, 17, 32, 47, 89, 160, 267] 401 [2, 3, 9, 11, 73, 89, 267] 402 [4, 5, 7, 11, 12, 23, 35, 73, 115, 161, 268] 403 [2, 3, 5, 7, 23, 26, 35, 62, 115, 161, 269] 404 [3, 8, 269] 405 [2, 6, 10, 18, 30, 54, 90, 162, 270] 406 [3, 4, 28, 116, 271] 407 [2, 3, 5, 22, 74, 163, 271] 408 [5, 16, 19, 43, 48, 163, 272] 409 [2, 3, 7, 9, 13, 19, 21, 39, 43, 63, 91, 117,
273] 410 [3, 4, 7, 9, 13, 20, 21, 39, 63, 91, 117,
164, 273] 411 [2, 6, 274] 412 [3, 5, 8, 11, 15, 25, 33, 55, 75, 165, 275] 413 [2, 3, 5, 11, 14, 15, 25, 33, 55, 75, 118,
165, 275] 414 [4, 12, 36, 92, 276] 415 [2, 3, 10, 166, 277] 416 [3, 7, 17, 49, 64, 119, 277] 417 [2, 5, 6, 7, 17, 49, 119, 167, 278] 418 [3, 4, 5, 9, 27, 31, 44, 76, 93, 167, 279] 419 [2, 3, 9, 27, 31, 93, 279] 420 [8, 24, 29, 40, 56, 120, 168, 280] 421 [2, 3, 29, 281] 422 [3, 4, 5, 13, 65, 169, 281] 423 [2, 5, 6, 7, 11, 13, 18, 65, 77, 94, 121,
169, 282] 424 [3, 7, 11, 16, 77, 121, 283] 425 [2, 3, 10, 23, 34, 37, 50, 170, 283] 426 [4, 12, 23, 37, 284] 427 [2, 3, 5, 9, 14, 15, 19, 45, 57, 95, 122,
171, 285] 428 [3, 5, 8, 9, 15, 19, 45, 57, 95, 171, 285] 429 [2, 6, 22, 26, 66, 78, 286] 430 [3, 4, 7, 20, 21, 41, 123, 172, 287] 431 [2, 3, 7, 21, 41, 123, 287] 432 [5, 32, 96, 173, 288] 433 [2, 3, 5, 17, 51, 173, 289] 434 [3, 4, 11, 17, 28, 51, 79, 124, 289] 435 [2, 6, 10, 11, 13, 30, 58, 67, 79, 174, 290] 436 [3, 8, 9, 13, 67, 97, 291] 437 [2, 3, 5, 7, 9, 25, 35, 38, 46, 97, 125, 175,
291] 438 [4, 5, 7, 12, 25, 35, 125, 175, 292] 439 [2, 3, 293] 440 [3, 16, 80, 176, 293] 441 [2, 6, 14, 18, 42, 98, 126, 294] 442 [3, 4, 5, 15, 52, 59, 68, 177, 295] 443 [2, 3, 5, 15, 59, 177, 295] 444 [7, 8, 24, 127, 296] 445 [2, 3, 7, 9, 10, 11, 27, 33, 81, 99, 127,
178, 297] 446 [3, 4, 9, 11, 19, 27, 33, 47, 81, 99, 297] 447 [2, 5, 6, 19, 47, 179, 298] 448 [3, 5, 13, 23, 39, 69, 128, 179, 299] 449 [2, 3, 13, 23, 29, 31, 39, 69, 299] 450 [4, 12, 17, 20, 29, 31, 36, 53, 60, 100, 180,
300] 451 [2, 3, 7, 17, 21, 22, 43, 53, 82, 129, 301] 452 [3, 5, 7, 8, 21, 43, 129, 181, 301] 453 [2, 5, 6, 181, 302] 454 [3, 4, 9, 101, 303] 455 [2, 3, 9, 10, 14, 26, 70, 101, 130, 182, 303] 456 [11, 16, 48, 83, 304] 457 [2, 3, 5, 11, 15, 61, 83, 183, 305] 458 [3, 4, 5, 7, 15, 61, 131, 183, 305] 459 [2, 6, 7, 18, 34, 54, 102, 131, 306] 460 [3, 8, 40, 184, 307] 461 [2, 3, 13, 71, 307] 462 [4, 5, 12, 13, 25, 28, 37, 44, 71, 84, 132,
185, 308] 463 [2, 3, 5, 9, 25, 37, 103, 185, 309] 464 [3, 9, 32, 103, 309] 465 [2, 6, 7, 10, 19, 30, 49, 62, 133, 186, 310] 466 [3, 4, 7, 19, 49, 133, 311] 467 [2, 3, 5, 11, 17, 55, 85, 187, 311] 468 [5, 8, 11, 17, 24, 55, 72, 85, 104, 187, 312] 469 [2, 3, 14, 134, 313] 470 [3, 4, 20, 188, 313] 471 [2, 6, 23, 41, 314] 472 [3, 5, 7, 9, 15, 16, 21, 23, 27, 35, 41, 45,
63, 105, 135, 189, 315] 473 [2, 3, 5, 7, 9, 15, 21, 22, 27, 35, 45, 63,
86, 105, 135, 189, 315] 474 [4, 12, 13, 73, 316] 475 [2, 3, 10, 13, 38, 50, 73, 190, 317] 476 [3, 8, 56, 136, 317] 477 [2, 5, 6, 18, 106, 191, 318] 478 [3, 4, 5, 11, 29, 33, 87, 191, 319] 479 [2, 3, 7, 11, 29, 33, 87, 137, 319] 480 [7, 31, 64, 137, 192, 320] 481 [2, 3, 9, 26, 31, 74, 107, 321] 482 [3, 4, 5, 9, 107, 193, 321] 483 [2, 5, 6, 14, 42, 46, 138, 193, 322] 484 [3, 8, 17, 19, 51, 57, 88, 323] 485 [2, 3, 10, 17, 19, 51, 57, 194, 323] 486 [4, 7, 12, 36, 108, 139, 324] 487 [2, 3, 5, 7, 13, 15, 25, 39, 65, 75, 139,
195, 325] 488 [3, 5, 13, 15, 16, 25, 39, 65, 75, 195, 325] 489 [2, 6, 11, 89, 326] 490 [3, 4, 9, 11, 20, 28, 89, 109, 140, 196, 327] 491 [2, 3, 9, 109, 327] 492 [5, 8, 24, 197, 328] 493 [2, 3, 5, 7, 21, 34, 47, 58, 141, 197, 329] 494 [3, 4, 7, 21, 23, 43, 47, 52, 76, 141, 329] 495 [2, 6, 10, 18, 22, 23, 30, 43, 66, 90, 110,
198, 330] 496 [3, 32, 331] 497 [2, 3, 5, 14, 142, 199, 331] 498 [4, 5, 12, 199, 332] 499 [2, 3, 9, 27, 37, 111, 333] |
|
3 1 5 2 7 3 13 4 17 5 32 6 38 7 67 9 |
137 11 203 13 247 15 472 17 578 18 682 19 787 21 1463 23 |
2047 25 2363 27 3465 29 5197 33 5198 35 8662 39 13513 41 15593 43 |
22522 49 22523 51 29452 55 60638 59 67567 65 67568 67 98753 69 112612 73 |
157658 79 202702 85 337837 97 337838 99 427927 103 713212 107 788287 109 788288 111 |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |