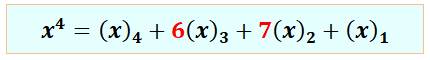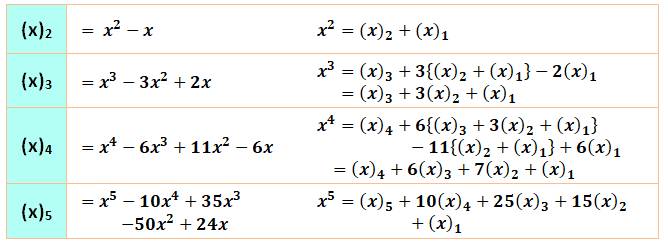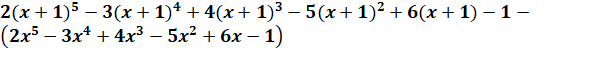NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/08/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	COMPTER - Combinatoire
Débutants Dénombrement	FACTORIELLES				Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Introduction		Tronquées	Généralisées
		Alternée	Tables des tronquées		Sous-factorielle
		Somme = 1/2	Nombres de Stirling 1		Stirling 2
		Sommaire de cette page >>> Nombres de Stirling de deuxième espèce

FACTORIELLE TRONQUÉE

Nombres de Stirling

(Deuxième espèce)

Ce sont en quelque sorte les réciproques des nombres de Stirling de la première espèce: la seconde espèce expriment la valeur d'une puissance en fonction des nombres de la première espèce.

Exemple:

Les coefficients 6 et 7 sont des nombres de Stirling 2.

Anglais: Generalized factorials: n factors, each one less than the preceding

Nombres de Stirling de deuxième espèce
Les nombres de Stirling 2 (valeur d'une puissance) se calculent en reprenant les nombres de Stirling 1 (valeur de la somme alternée de puissances).	Stirling 1 (x)1 = x (x)2 = x² – x	Stirling 2 x = (x)1 x² = (x)2 + (x)1
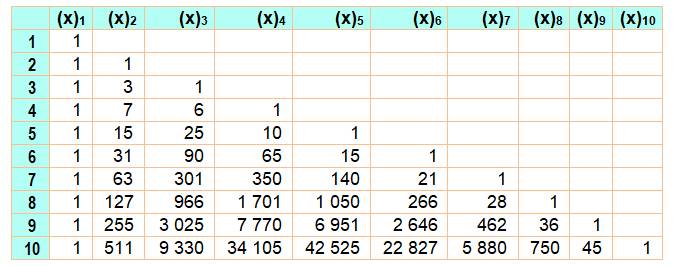
Calcul des premières valeurs Tableau des nombres de Stirling 2 jusqu'à n = 10

Calcul de différence finie
Soit le polynôme
Calculez la différence finie première	Après développements des puissances:
Avec les nombres de Stirling, on propose une autre méthode de calcul basée sur une double transformation: polynôme puissance en polynôme factorielles, puis retour aux puissances.
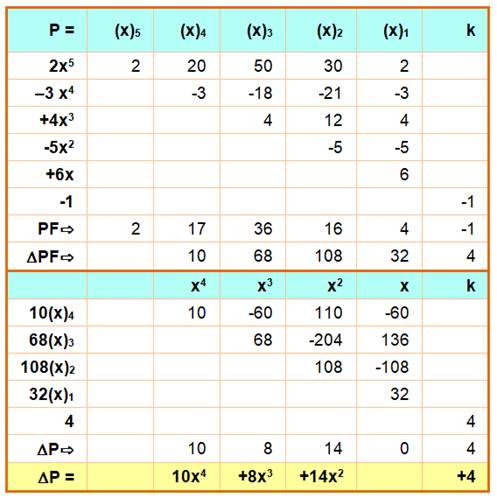
1) Première transformation en factorielles tronquées et avec les nombres de Stirling 2. 2) On prend la différence finie de PF. Exemple pour 2(x)5 => 5 fois la différence précédente, soit 10(x)4 . 3) on repasse aux valeurs des puissances avec les nombres de Stirling 1. La somme restitue bien le polynôme calculé directement

Retour	Nombres de Stirling de première espèce
Suite	Somme et produit de 3 nombres consécutifs Division des factorielles tronquées Factorielle tronquée = carré? Factorielles généralisées Produit de k nombres consécutifs – Divisibilité
Voir	Coefficient du binôme Constante "e" Constante "pi" Factorielles divisées Loto Partition en nombres consécutifs Programmation du calcul des factorielles Théorie des nombres – Index
Sites	Nombres de Stirling – Wikipédia OEIS A008275 – Triangle read by rows of Stirling numbers of first kind, s(n,k), n >= 1, 1<=k<=n. OEIS A008275 – Triangle of Stirling numbers of first kind, s(n, n-k+1), n >= 1, 1 <= k <= n.
DicoNombre	Nombre 3 Nombre 6 Nombre 10 Nombre 11	Accès à tous les Nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/Stirlin2.htm