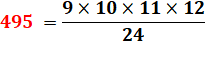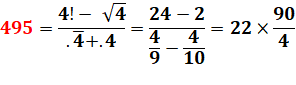Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 08/05/2025 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100 / 200 / 300			400 à 499		500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	400	410	420	430	440	450	460	470	480	490
	490	491	492	493	494	495	496	497	498	499

Quatre-cent-quatre-vingt-quinze

Quatre-cent-nonante-cinq

Four hundred ninety-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	111101111Palindrome
Bases	7578 35312 17119
Romain	CD XC V

Suite

Composé

Congruent

Déficient

Fourchette ou gapful

Impair

Interpremier (491, 499)

Kaprekar (procédé)

Palindrome en binaire

Pentatope

Géométrique

2-pentagonal

Chiffres et numération

495 / 45 = 11	Nombre fourchette.
495 = 1111 0 11112	Palindrome en binaire.
495 = 954 – 459	Seule forme de ce type: différence de ses anagrammes – Voir 954
495 + 594 = 1089 = 33² 495 – 594 = –99	Devient carré en lui ajoutant son retourné et repdigit en lui retirant.
49510 = [2, 12, 1]13 = [1, 12, 2]17 = [1, 2, 12]21	Même jeu de chiffres en bases 13, 17 et 21

Addition et soustraction

495 = 2 + 3 + … + 31 = 40 + 41 + … + 50		Une des ONZE sommes de nombres consécutifs >>> Un autre exemple pour ses extrémités remarquables.
495 = 19 + 20 + … + 36		Nombre 2-pentagonal: somme des dix-huit nombres supérieurs à 18.
495 = 45 + 46 + … + 54 = 55 x 9		Somme de consécutifs, égale à un multiple du nombre suivant.
495 = 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) + 9x50			Forme pannumérique divisible par 9.
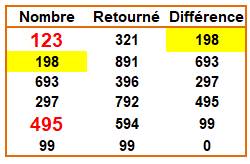
495 = 954 – 459	Nombre limite du procédé de Kaprekar pour les nombres à trois chiffres. Pour quatre chiffres, c'est 6 174. Principe du procédé ou impasse de Kaprekar Procédé itératif pour lequel La différence entre le nombre et son retourné est utilisé pour créer le nombre suivant auquel les mêmes opérations sont appliquée. Avec trois chiffres, le procédé conduit au nombre 495. Ce résultat est obtenu en cinq itérations au maximum Il existe des cas particuliers conduisant à 0. Exemple: 102, 198, 792, 693, 594, 495. Principe du calcul: 102 => 210 – 12 = 198 => 981 – 189 = 792 …

Multiplication et division

495 = 3² x 5 x 11	Facteurs. Pentatope
	Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
	Doublet de nombres en phi (quantité de premiers avec lui et inférieurs à lui).

Avec les puissances

495 = 7² + 10² + 11² + 15²	Une des sommes de quatre carrés >>>
495 = 7² + 9² + 10² + 11² + 12²	Somme de carrés de nombres distincts (exemple).
495 = 3^3 + 5^3 + 7^3	Somme des cubes des trois plus petits premiers impairs.

Dénombrement, jeux et curiosités

	Jeu du quatre 4. Avec la notation .4 = 0,4 = 4/10 et .4 surligné = 0,444… = 4/9
	Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 4 parmi 12. Exemple de simplification pour faciliter le calcul

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 1, 0, 1, 1, 1, 1] 3, [2, 0, 0, 1, 0, 0] 4, [1, 3, 2, 3, 3] 5, [3, 4, 4, 0] 6, [2, 1, 4, 3] 7, [1, 3, 0, 5] 8, [7, 5, 7] 9, [6, 1, 0] 10, [4, 9, 5] 11, [4, 1, 0]	12, [3, 5, 3] 13, [2, 12, 1] 14, [2, 7, 5] 15, [2, 3, 0] 16, [1, 14, 15] 17, [1, 12, 2] 18, [1, 9, 9] 19, [1, 7, 1] 20, [1, 4, 15] 21, [1, 2, 12]	22, [1, 0, 11] 23, [21, 12] 24, [20, 15] 25, [19, 20] 26, [19, 1] 27, [18, 9] 28, [17, 19] 29, [17, 2] 30, [16, 15] 60, [8, 15]	32, [15, 15] 44, [11, 11] 54, [9, 9] 98, [5, 5] 164, [3, 3] 494, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombres en 480 Nombres en 500
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb400/Nb495.htm