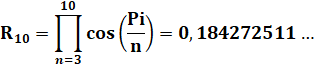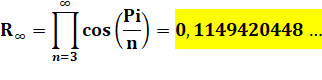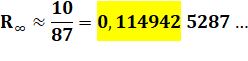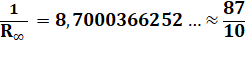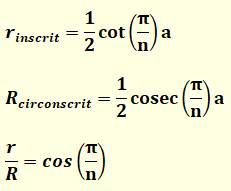Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 09/02/2024 M'écrire Brèves de Maths

INDEX Polygone Géométrie Défis en géométrie	Polygones
	Polygones	Polyèdres	Polytopes
	Polygones – Propriétés	Tectoèdres	Golygones
	Polygones gigognes	Holyèdres	Polygones concaves

Faites un double-clic pour un retour en haut de page

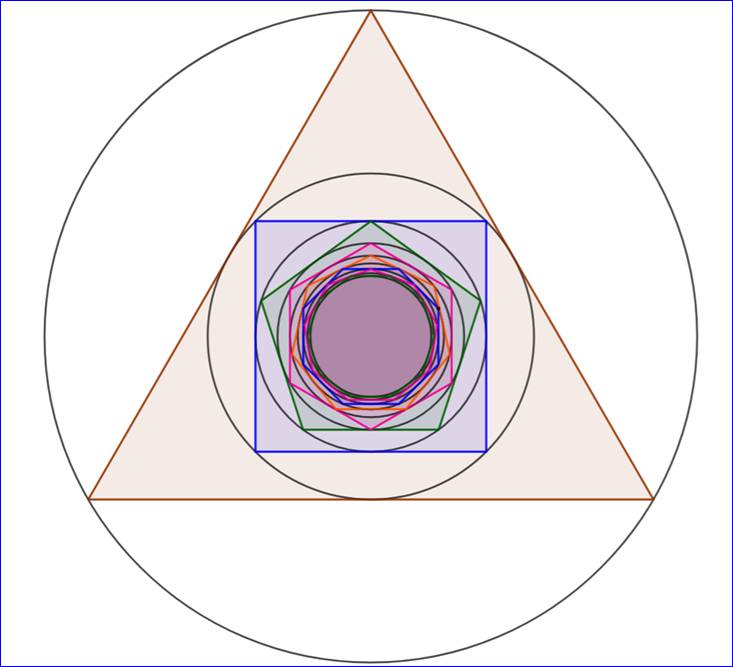
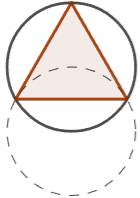
Polygones gigognes Constante de Kepler-Bouwkamp À partir du triangle isocèle, les polygones réguliers avec de plus en plus de côtés sont construits les uns emboités dans les autres. On cherche la propriété de convergence des rayons des cercles circonscrits et inscrits. Convergence observée vers une constante valant 0,1149420448… ou son inverse 8,70003… selon le sens de l'emboitement.
	Sommaire de cette page >>> Approche – Construction >>> Construction du pentagone et suite >>> Polygones gigognes jusqu'au décagone >>> Constante de Kepler-Bouwkamp	Débutants Géométrie Glossaire Géométrie

Approche – Construction		haut
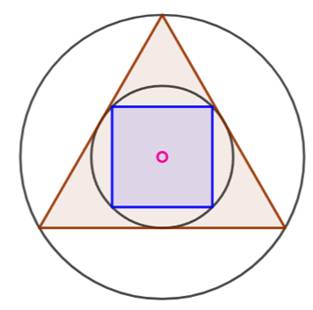
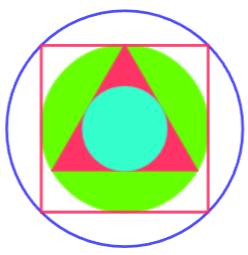
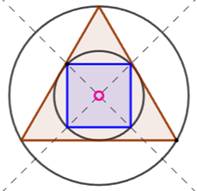
Triangle équilatéral et carré Au départ, un cercle unité. Le triangle équilatéral inscrit Sa construction est simple avec un cercle identique centré sur le cercle initial. Pour le cercle inscrit dans le triangle, du centre du cercle, tracer une perpendiculaire au côté. Le point d'intersection est l'extrémité du rayon du cercle cherché. La construction du carré consiste à dessiner les deux droites à 45° passant par le centre. Les points d'intersection avec petit le cercle sont les sommets du carré.

Voir Constructions – Index

Construction du pentagone et suite		haut
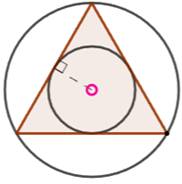
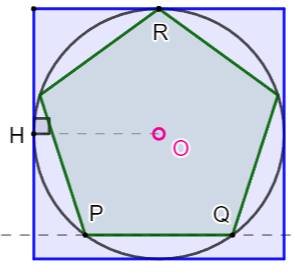
Cercle inscrit au carré Pour le cercle inscrit, du centre du cercle, tracer une perpendiculaire au côté. Le point d'intersection H est l'extrémité du rayon OH du cercle cherché. Pentagone Il est bien entendu possible de construire un pentagone exact. Ici, nous allons, utiliser les facilités de GeoGebra, y compris de sa fonction zoom. Choisir un point P sur l'objet cercle. Tracer la parallèle au côté du carré qui produit le point Q. Avec l'outil polygone, créer un pentagone ayant PQ pour côté. Sa taille est quelconque pour le moment. Faire glisser le point P sur le cercle pour ajuster le point R sur le cercle. Utiliser le zoom pour un ajustement très précis. Hexagone et suite Utiliser ces mêmes constructions pour tracer la suite des cercles concentriques et des polygones gigognes.

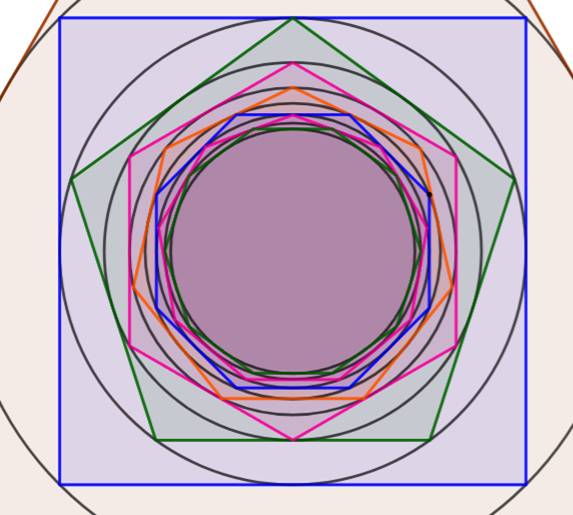
Polygones gigognes jusqu'au décagone

Zoom interne au carré

Constante de Kepler-Bouwkamp		haut
Convergence Le tracé de la figure montre que les cercles et polygones deviennent de plus en plus petits. On sait calculer le rayon des cercles. Quelle est le rayon limité pour une quantité infinie de côtés ? Constante de Kepler-Bouwkamp C'est le produit du rapport entre deux cercles successifs Pour aller au décagone, on aura: Pour la limite, on a la constante de Kepler-Bouwkamp: Figure inverse En fait, Bouwkamp part du triangle équilatéral et l'entoure de son cercle circonscrit et de la suite des polygones et cercles. Il calcule le rayon du cercle qui grossit pour atteindre une limite, laquelle est l'inverse de la constante:	Rayons des cercles inscrits et circonscrits Voir Polygones Historique Nommé d'après Kepler (1571-1630) qui avait eu l'idée d'emboiter les volumes et de leur donner une signification planétaire. Christoffel Bouwkamp est un mathématicien astronome néerlandais (1915-2003). Approche de Bouwkamp

Anglais: Kepler-Bouwkamp or polygon-inscribing constant

Haut de page (ou double-clic)

Retour	Polygones
Suite	Polygones – Propriétés Diagonales dans les polygones Régions et intersections dans les polygones Groupe de symétrie des polygones réguliers
Voir	Géométrie – Index Illusions d'optique Polyèdres Polygones magiques Triangles
Sites	Constante de Kepler-Bouwkamp – Wikipédia OEIS A085365 – Decimal expansion of the Kepler-Bouwkamp or polygon-inscribing constant OEIS A051762 – Polygon circumscribing constant: decimal expansion of Product_{n>=3} 1/cos(Pi/n) Circles, polygons and the Kepler-Bouwkamp constant – ThatsMaths – Peter Lynch Polygon Inscribing – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/PolyGigo.htm