|
||||||||||||||||||||||||||||||
![]()
|
POLYGONES Réguliers Méthode générale de construction
approchée Méthode très approximative,
mais simple et applicable à tous les polygones réguliers. |
Voir Méthode
Bion de construction approchée des polygones
Semblable à celle exposée ici.
|
|
|||
|
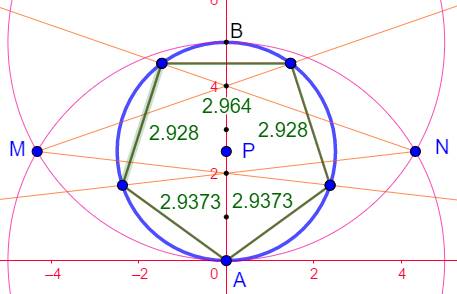
Construction Sur une
demi-droite AB, report 5 fois de la même distance. Points
notés de 0 à 5. Le point P est le milieu. Cercle en bleu (P, PA). Cercles
(A, AB) et (B, AB); intersections M et N. Demi-droites
à partir de M vers les numéros pairs et même chose à partir de N. Les
points d'intersections avec le cercle bleu sont les sommets du pentagone
approché. |
|
||
|
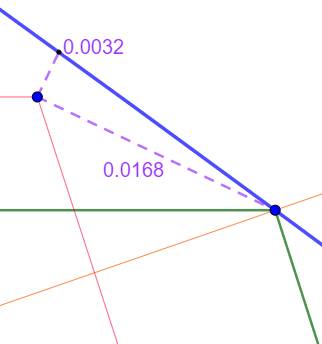
Appréciation En vert, le pentagone approximatif En rouge, un pentagone régulier ayant A pour
sommet. En bleu, le cercle circonscrit. Zoom sur le sommet opposé de droite. Pour une longueur du côté proche de 3, la distance
entre les sommets vaut: 0,0168. Erreur relative de 0,6 % |
|
||
Voir Construction
du pentagone
|
|
|
|
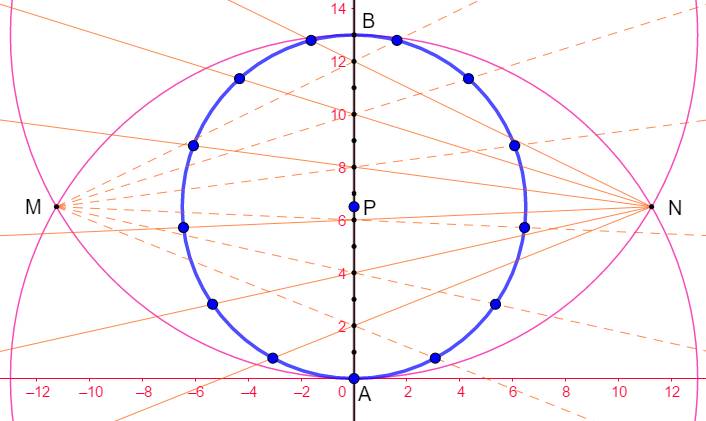
Construction Sur une
demi-droite AB, report 13 fois de la même distance. Points
notés de 0 à 13. Le point P est le milieu. Cercle en bleu (P, PA). Cercles
(A, AB) et (13, AB); intersections M et N. Demi-droites
à partir de M vers les numéros pairs et même chose à partir de N. Les
points d'intersections avec le cercle bleu sont les sommets du tridécagone
approché.
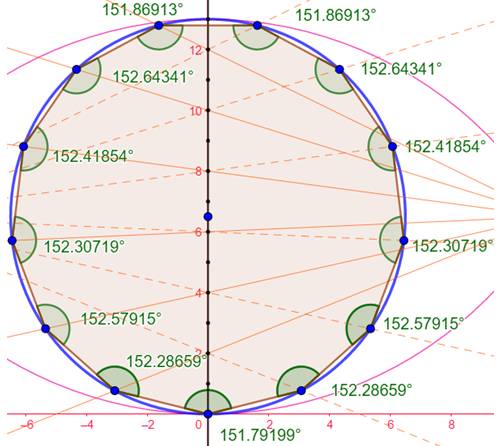
Appréciation Comme le
montre ce relevé des angles, le tridécagone régulier est très approximatif.
De 151,86°
à 152,64°, soit 0,78° d'écart. Erreur relative de 0,5 %. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Document |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Poly13CG.htm
|
![]()