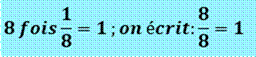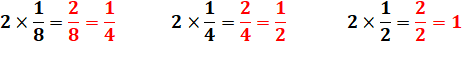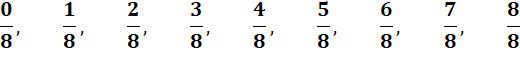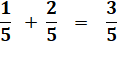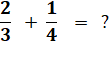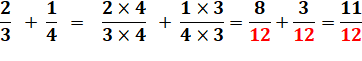|
Édition du: 06/04/2020 |
![]()
|
FRACTIONS – Avec briques Il arrive
très souvent qu'un enfant ne comprenne pas l'idée de fraction. Mal
appréhendée au départ, et le calcul fractionnaire deviendra un cauchemar qui
va s'éterniser jusqu'en cinquième,
voire au-delà. Comment créer le déclic de la compréhension ? Le même
phénomène existe plus tard au lycée avec la notion de vecteur. Exemple de calcul avec les briques du jeu de construction de
type LegoTM.
|
||
|
|
Sommaire de cette page >>> Le problème du débutant >>> Quelques fractions en huitièmes >>> Exemple d'opérations avec des cinquièmes >>> Opérations mixtes >>> Bilan |
Débutants Glossaire |
|
Constat D'après mon expérience, le débutant a du mal à
imaginer que la fraction est une entité en soi. Le fait qu'il y ait deux nombres le déroute. Il
les manipule un peu au hasard sans bien comprendre à quoi ils correspondent. Les analogies aident à créer le déclic de
compréhension, le "Ah, ah, ça y est j'ai compris". Analogies Avec certains, la lecture des heures sur l'horloge
va faire connaitre immédiatement les fractions un demi, un quart et un tiers. L'analogie des briques de type Lego ou la méthode
Singapour
sont aussi de bons moyens pour visualiser le processus de fraction. J'ai connu d'autres enfants plus difficiles à
convaincre et qui n'ont eu le déclic
qu'avec l'analogie des bêtes à antennes
et à pattes, méthode que j'ai inventée pour bien faire réaliser que la
fraction est un tout. |
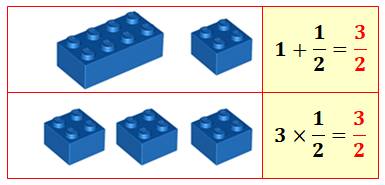
La fraction un-huitième Illustrée par un seul élément sur une plaque qui
peut en contenir huit.
À gauche, le remplissage n'est que de un sur huit. On écrit ce que l'on vient de dire:
On note (à droite) que le remplissage huit fois un sur huit
équivaut à une plaque pleine:
|
|
|
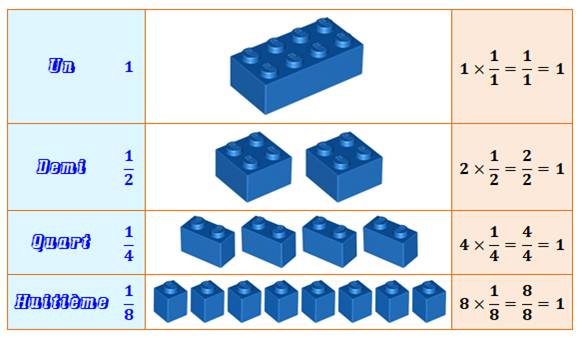
La brique de base représente une unité. Ici elle
possède huit emplacements propices à définir quelques fractions. La brique de base est FRACTIONNÉE
en 2, 4 ou 8. Fractionnée en deux, on obtient deux
demi-briques; lesquelles emboitées sur la brique de base, la couvrent
complètement: deux demis égal un. |
Principe du fractionnement de la
brique de base
Note: rien n'empêche de prendre une brique de base
avec deux fois plus d'emplacements, comme si chaque emplacement d'origine
était divisé en deux. Alors, on crée des seizièmes. |
|
|
Voyez comment, avec deux briques d'un niveau on
crée une brique du niveau du dessus. |
Équivalences
|
|
|
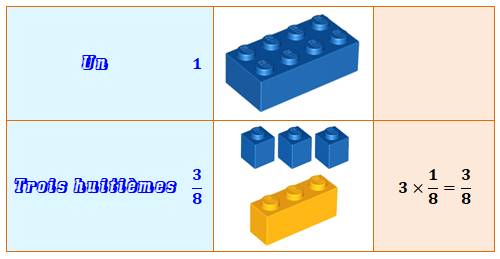
Toujours avec la brique de base à huit emplacements,
en choisissant d'en remplir trois, par exemple, on forme simplement la
fraction trois huitièmes. On peut les voir séparément: 3 fois un huitième;
ou alors réunis en un seul bloc qui vaut trois huitièmes. |
Fraction bizarre ! Mais tout à fait
légitime.
|
|
|
Il existe neuf fractions en huitièmes En vous aidant de la représentation en briques,
vous pourrez simplifier les fractions |
Toutes les fractions en huitièmes
|
|
|
Les fractions en cinquième La brique de base peut être quelconque. Exemple
avec une plaque munie de cinq emplacements de billes (en orange). Elle sert à former les fractions en cinquièmes
selon le nombre de billes déposées (noires). Par exemple, si on pose trois billes noires, on
occupe trois sur cinq emplacements et la fraction est 3/5. |
|
|
|
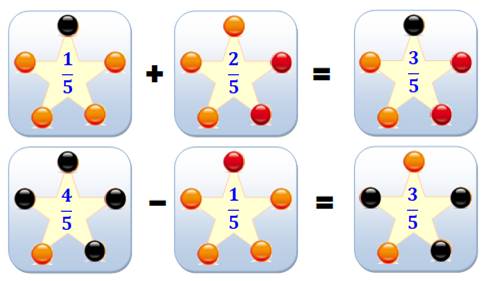
Addition et soustraction imagées Je forme deux fractions en posant une bille sur
une plaque et en posant deux billes sur l'autre; j'ai évidemment posé trois
billes. Les fractions, c'est aussi simple que cela. |
|
|
|
Addition des fractions Dans le monde des cinquièmes,
l'addition se fait normalement en gardant le mot cinquième comme s'il s'agissait
d'une unité (comme des kilogrammes ou des mètres carrés). |
On aurait très bien pu choisir
de noter: 1 5e + 2 5² = 3 5e Mais, cette notation n'est pas
très lisible. |
|
|
Possible ? Pas en l'état ! On ne peut pas mélanger les tiers et les quarts. |
|
||
|
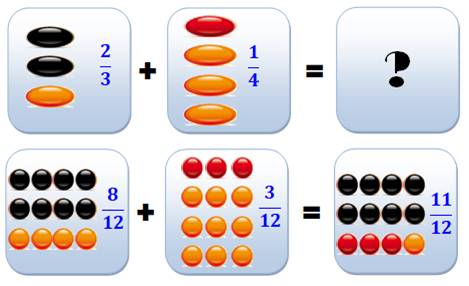
Solution: fractionner plus petit Au lieu de prendre une plaque de tiers et une
plaque de quarts qui sont incompatibles, on s'arrange pour trouver une plaque
qui convienne aux deux. Ce sera une plaque de douzièmes (en effet: 3 x 4
= 12). Sur la plaque des tiers, les trois emplacements
sont fractionnés en quatre pour faire douze emplacements. Sur la plaque des quarts, les quatre emplacements
sont fractionnés en trois pour faire douze emplacements. Les billes posées (noires et rouges) sont fractionnées
de la même manière. |
En orange, les emplacements
de billes, et en noir ou en rouge les billes
posées. Deux billes posées sur trois emplacements forment la fraction
2/3.
|
||
|
Maintenant, avec des plaques identiques en
douzièmes, l'addition est possible. |
|
||
|
Comparez On n'ajoute pas des kilogrammes et des grammes; |
3 kg + 150 g = ? 3000 g + 150 g = 3150 g |
||
Voir Calcul avec même dénominateur
|
Brique
type Lego La quantité
d'emplacements sur la brique s'appelle le dénominateur. Le nombre
d'emplacements couverts s'appelle le numérateur. |
Plaque
et billes La quantité
d'emplacements de billes sur la plaque s'appelle le dénominateur. Le nombre de
billes posées s'appelle le numérateur. |
|
|
|
![]()
|
|
|
|
|
Voir |
||
|
DicoNombre |
||
|
Site |
|
|
|
Vidéos |
Vidéos
pour apprendre les fractions avec des Legos: quelques exemples de sites; il
en existe beaucoup d'autres.
|
|
|
Cette page |
||