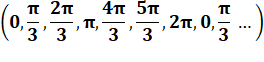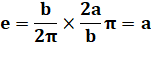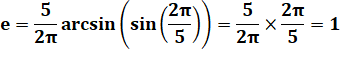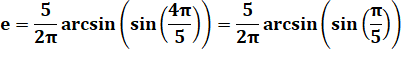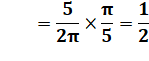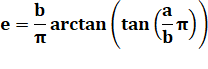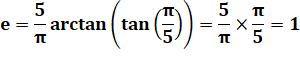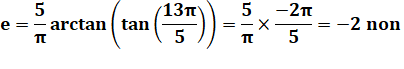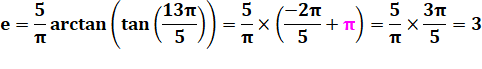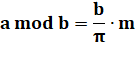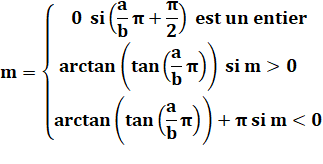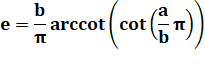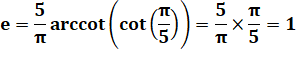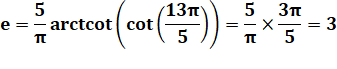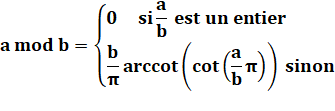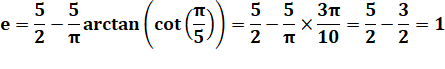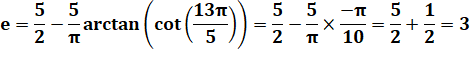NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/09/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	CALCULS SIMPLES				Glossaire Général
INDEX Trigonométrie Multiplication	Trigo	Pentes	Exemple	Avancés
	Multiplication via la trigonométrie		Congruence avec trigonométrie
		Sommaire de cette page >>> Principe >>> Expression avec sinus ou cosinus >>> Allure cyclique des fonctions trigonométriques >>> Expression avec tangente seule >>> Expression avec cotangente seule >>> Expression avec tangente et cotangente

Congruence exprimée par lignes trigonométriques

La fonction modulo compte, par exemple de cette manière (1, 2, 3, 4, 0, 1, 2 …), sorte de va-et-vient linéaire sur la droite des nombres.

L'expression d'un angle tourne sur le cercle en une sorte de mouvement circulaire, par exemple:

Comment exprimer l'un (linéaire) avec l'autre (circulaire) ?

Résultat: deux relations intéressantes (sauf exceptions pour cas particuliers):

Principe

L'idée est double:

profiter des propriétés modulo 2 des angles pour exprimer les nombres entiers modulo k, et

prendre une ligne trigonométrique d'un angle (le sinus, par exemple) et de revenir à l'angle par la fonction inverse (l'arcsinus).

Oui, mais les fonctions trigonométriques comme le sinus sont "réversibles" sur 90° (isomorphisme: à chaque angle est associée une valeur de sinus), mais pas sans doublons sur 360° (1/2 est le sinus de 30° et de 150°).

La tangente semble la fonction la plus appropriée.

Expression avec sinus ou cosinus
Faisons cette proposition avec les paramètres a et b, et vérifions l'égalité entre m et e.
Si on oublie les transformations on a: e = a. L'idée est que les transformations réalisent une fonction modulo b. Est-ce réalisable avec les sinus ?
a = 1 et b = 5 OUI	m = 1 mod 5 = 1
a = 2 et b = 5 NON	m = 2 mod 5 = 2
Ces deux fonctions, sinus et cosinus, ne se prêtent pas à une rotation sympathique.		Par exemple, le sinus retrouve les mêmes valeurs par symétrie verticale sur le cercle trigonométrique. Impossible d'exprimer un modulo avec ces deux fonctions.

Allure cyclique des fonctions trigonométriques

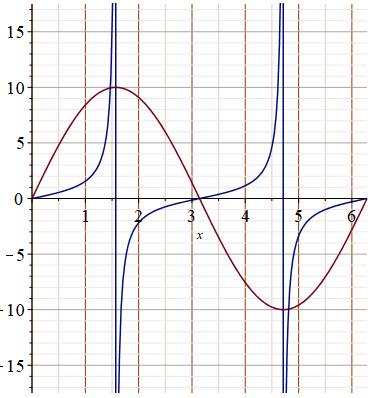
Nous venons de voir que la fonction sinus n'est pas adaptée à une représentation cyclique sur un tour (2Pi): la fonction passe quatre fois par la même valeur positive ou négative. La fonction tangente est plus propice, même si elle a l'inconvénient de s'enfuir vers l'infini pour Pi/2 et 3Pi/2. Idem pour cotangente avec exception en k.Pi

Graphe 10 x sinus et tangente

Expression avec tangente seule
Faisons cette proposition avec les paramètres a et b et vérifions l'égalité. Note: le cas b = 0 est bien sûr exclu.
a = 1 et b = 5 OUI	m = 1 mod 5 = 1
a = 13 et b = 5 OUI avec ajout de Pi	m = 13 mod 5 = 3 et c'est aussi – 2 mod 5
Bilan Formule valable mais il faut tenir compte des valeurs critiques avec: tan(k.Pi+Pi/2) impossible. Pour les angles dans les deux quadrants du bas, ajouter Pi.
Vérification par logiciel (a, b, m, e) a et b de 1 à 5		1, 1, 0, 0 1, 3, 1, 1 1, 4, 1, 1 1, 5, 1, 1 2, 1, 0, 0		2, 2, 0, 0 2, 3, 2, 2 2, 5, 2, 2 3, 1, 0, 0		3, 3, 0, 0 3, 4, 3, 3 3, 5, 3, 3 4, 1, 0, 0	4, 2, 0, 0 4, 3, 1, 1 4, 4, 0, 0 4, 5, 4, 4	5, 1, 0, 0 5, 3, 2, 2 5, 4, 1, 1 5, 5, 0, 0

Expression avec cotangente seule
Faisons cette proposition avec les paramètres a et b et vérifions l'égalité.
a = 1 et b = 5 OUI	m = 1 mod 5 = 1
a = 13 et b = 5 OUI	m = 13 mod 5 = 3
Bilan Formule valable mais il faut tenir compte des valeurs critiques avec: cotan(k.Pi) impossible.
Vérification par logiciel (a, b, m, e) a et b de 1 à 5		1, 2, 1, 1 1, 3, 1, 1 1, 4, 1, 1		1, 5, 1, 1 2, 3, 2, 2 2, 4, 2, 2	2, 5, 2, 2 3, 2, 1, 1 3, 4, 3, 3	3, 5, 3, 3 4, 3, 1, 1 4, 5, 4, 4	5, 2, 1, 1 5, 3, 2, 2 5, 4, 1, 1

Expression avec tangente et cotangente
Faisons cette proposition avec les paramètres a et b et vérifions l'égalité.
a = 1 et b = 5 OUI	m = 1 mod 5 = 1
a = 13 et b = 5 OUI	m = 13 mod 5 = 3
Bilan Formule valable mais il faut tenir compte des valeurs critiques comme: tan(Pi/2 + k.Pi) impossible et cotan(k.Pi) impossible.
Vérification par logiciel (a, b, m, e) a et b de 0 à 5		0, 1, 0, 0 0, 2, 0, 0 0, 3, 0, 0 0, 4, 0, 0 0, 5, 0, 0		1, 1, 0, 0 1, 2, 1, 1 1, 3, 1, 1 1, 4, 1, 1 1, 5, 1, 1	2, 1, 0, 0 2, 2, 0, 0 2, 3, 2, 2 2, 4, 2, 2 2, 5, 2, 2	3, 1, 0, 0 3, 2, 1, 1 3, 3, 0, 0 3, 4, 3, 3 3, 5, 3, 3	4, 1, 0, 0 4, 2, 0, 0 4, 3, 1, 1 4, 4, 0, 0 4, 5, 4, 4	5, 1, 0, 0 5, 2, 1, 1 5, 3, 2, 2 5, 4, 1, 1 5, 5, 0, 0

Suite	Multiplication via la trigonométrie Calculs avec les arc tangentes Pente – Calcul avancé
Voir	Théorème de Pythagore Trigonométrie – Débutant Trigonométrie – Calculs avancés Trigonométrie – Formules
Aussi	Angle et cercle trigonométrique Unités
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/ModTrigo.htm