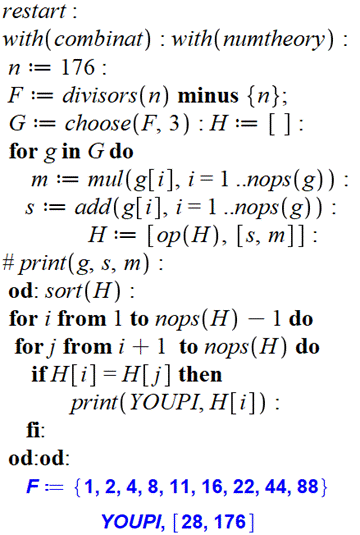|
Édition du: 24/05/2025 |
|
INDEX |
Égalités |
|||
![]()
|
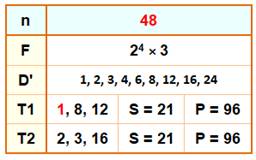
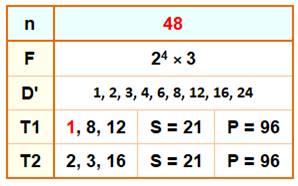
Sommes et produits identiques avec les diviseurs
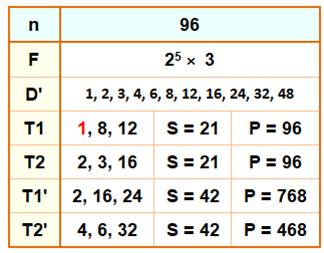
Considérant les
diviseurs d'un nombre et parmi les combinaisons de trois d'entre eux, on
cherche ceux ayant à la fois la même somme et le même produit. Le tableau donne
l'exemple du nombre 28 avec les deux triplets de diviseurs T1 et T2. On a les
égalités suivantes: S = 1 + 8 + 12 = 2 +
3 + 16 = 21 P = 1 × 8 × 12 = 2 × 3 × 16 = 96 |
||
|
|
Sommaire de cette page >>> Approche >>> Liste >>> Florilège >>> Programmation |
Débutants Glossaire |
|
Nombres recenseurs (sommes
et produits avec des nombres) >>> Nombres
dont le produit de trois facteurs peut s'exprimer de deux façons et tels que
les deux sommes de ces trois facteurs soient égales. n
= P = 72 = 2 ×
6 ×
6 = 3 × 3 ×
8 S = 2 + 6 +
6 = 3 + 3 +
8 = 14 Les
facteurs des produits peuvent être multiples La
paire de triplets est unique. |
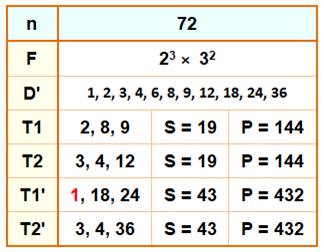
Nombres sommes-produits-diviseurs identiques (sommes
et produits avec les diviseurs) >>> Nombres
tels que deux triplest de diviseurs produisent la même somme et le même
produit. Diviseurs
de 72 = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24,
36} P
= 2 ×
8 ×
9 = 3 × 4 ×
12 = 144 S
= 2 +
8 +
9 = 3 + 4 +×
12 = 19 Les
facteurs des produits sont distincts. Plusieurs
paires de triplets autorisées. |
|
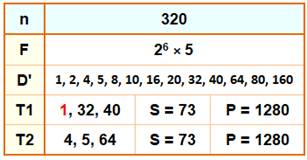
Exemple avec le nombre 176 On connait sa factorisation F. On connait la liste de ses diviseurs propres
(D'), sans y inclure le nombre lui-même. Parmi toutes les sommes de trois diviseurs, il en
existe une qui se produit deus fois tout en créant le même produit. Nous avons ainsi deux triplets de diviseurs (T1 et T2) avec même somme (28) et même produit (176). |
|
|
|
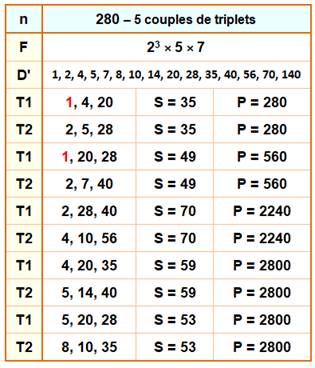
Exemple avec le nombre 72 Avec ce nombre, les égalités existent deux fois. |
|
|
|
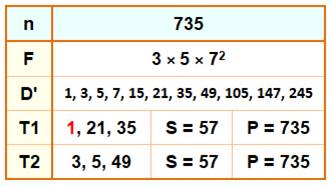
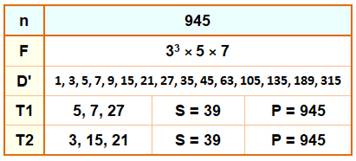
Exemple avec le nombre 735 Un exemple avec un nombre impair, cas moins
fréquent qu'avec les nombres pairs. |
|
|
|
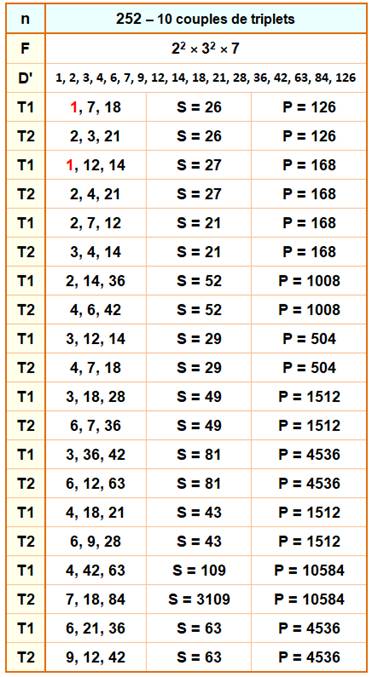
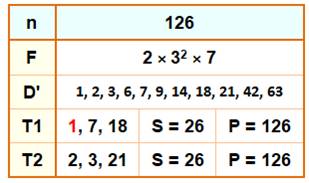
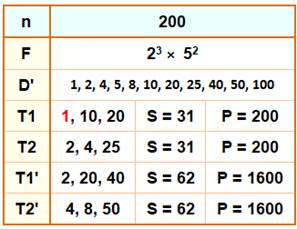
Liste de 1 à 1000 Nombres k fois double-triplets de mêmes sommes et mêmes produit de ses
diviseurs. Exemple avec 72 (explicité plus haut): il est deux fois triplets et
noté [72, 2]. En rouge, les nombres impairs. |
[48, 1], [60, 2], [72, 2], [84, 2], [90, 2],
[96, 2], [100, 1], [120, 8], [126, 1], [140, 1], [144, 8], [168, 5], [176, 1], [180, 15], [192, 4],
[198, 2], [200, 2], [210, 3], [216, 5], [240, 25], [252, 10], [260, 1],
[264, 2], [270, 7], [280, 5], [288, 16], [294, 1], [300, 8], [312, 1], [315, 1], [320, 1], [324, 1], [330, 3], [336, 18],
[350, 1], [352, 2], [360, 57], [378, 3], [384, 6], [390, 1], [396, 4], [400,
3], [408, 1], [420, 35], [432, 19], [440, 3], [448, 1], [450, 8], [462, 3],
[468, 2], [480, 47], [500, 2], [504, 40], [510, 2], [520, 2], [528, 9], [532,
1], [540, 41], [546, 3], [550, 1], [560, 15], [567,
1], [570, 2], [576, 26], [585, 1], [588, 7],
[594, 5], [600, 32], [612, 2], [616, 1], [624, 7], [630, 34], [640, 2], [648,
11], [650, 1], [660, 19], [672, 35], [675, 1],
[680, 1], [684, 1], [690, 1], [700, 8], [704, 4], [714, 1], [720, 146], [735,
1], [736, 1], [756, 29], [765, 2], [768, 8],
[770, 3], [780, 15], [784, 2], [792, 22], [800, 5], [810, 13], [816, 6], [819, 1], [828, 3], [840, 122], [855, 1], [858, 1], [864, 41], [880, 10], [882, 5],
[896, 2], [900, 60], [912, 4], [918, 2], [924, 16], [936, 17], [945,
4], [952, 1], [960, 74], [968, 1], [972, 2], [975,
1], [980, 3], [988, 1], [990, 27], [1000, 4], … |
|||
|
Records jusqu'à 10 000 Dans cette liste, le nombre suivant présente plus
de triplets que le précédent. |
[48, 1], [60, 2], [120, 8], [180, 15], [240, 25], [360, 57], [720,
146], [1080, 148], [1260, 196], [1440, 267], [1680, 318], [2160, 370], [2520,
641], [4320, 692], [5040, 1519], [7560, 1668], … |
|||
|
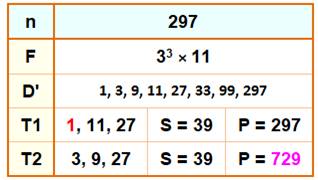
Liste stricte Cette liste est donnée en OEIS A334911.
Elle diffère de celle donnée ci-dessus pour deux raisons:
|
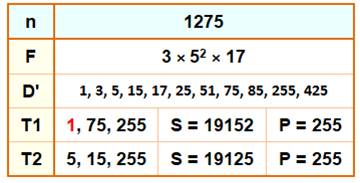
36, 40, 72, 96, 126, 176, 200, 225, 234,
252, 280, 297,
320, 408, 520, 550, 576, 588, 600, 648, 690, 714, 735, 736, 768, 780, 784, 816, 850, 855, 896, 945, 972, 1026, 1040, 1064,
1092, 1160, 1188, 1216, 1242, 1248, 1275, 1280, 1296, 1300, 1350, 1404, 1530 |
|||
|
Pairs
|
|
|
|
Impairs
Avec anagramme
|
|
|
|
|
But Identifier les triplets de diviseurs ayany mêmes
sommes et mêmes produit. Commentaires Appel aux logiciels de combinatoire et de théorie
des nombres. La liste F contient les diviseurs de n sauf n. La liste G contient toutes les combinaisons de
trois de ces diviseurs. Pour chacune (g) on calcule le produit (m) et la
somme (s). Ces valeurs sont mémorisées dans la liste H qui va être triée par
ordre croissant (sort). Cette liste de [produit-somme] est analysée à
l'aide de deux boucles pour détecter les égalités. Si c'est le cas,
impression du couple somme-produit. Un retraitement en forçant l'impression des
triplets de diviseurs permet de reconnaitre ceux concernés. Il n'est pas difficile
de programmer la recherche correspondante. |
|
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |