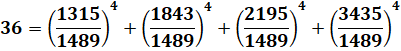Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 15/04/2025 M'écrire Brèves de Maths

INDEX Partitions Types de nombres	n = somme de puissances
	Entiers	Somme de 4 carrés Théorème de Lagrange	Somme de n puissances Théorème de Waring
	Somme de puissances 4	Sommes de carrés	Sommes de cubes
	Somme de puissances 5	Somme de puissances 5 - PN	Euro et Dollar

Faites un double-clic pour un retour en haut de page

Nombres P4 (puissance 4) Plusieurs points d'intérêts avec les puissances des nombres entiers: combien de puissances quatrièmes sont nécessaires au plus pour partitionner les nombres? quels sont les partitions des nombres en quatre puissances quatrièmes? Est-ce toujours possible? Quels sont les nombres plusieurs fois sommes de k puissances quatrièmes? Quels sont les puissances quatrièmes sommes de k puissances quatrièmes? On s'intéresse aux sommes de puissances quatrièmes des entiers; qu'ils soient positifs ou négatifs, la puissance 4 sera toujours positive. Bien ! Mais peut-on voir comment se comporte les nombres avec des additions et soustractions de puissances quatrièmes ? Pour une introduction et certaines curiosités avec les puissances quatrièmes, voir la page générale: Exemples
	Sommaire de cette page >>> Partitions en puissances quatrièmes >>> Tables des kP4 avec k nombres >>> Carrés = somme de P4 >>> Sommes de rationnels >>> Somme deux fois en P4	Débutants Nombres Glossaire Nombres

Voir Nombre 4

Partitions en puissances quatrièmes		haut
Théorème de Waring pour la puissance 4 Tout nombre entier est décomposable en sommes d'au plus 19 puissances cinquièmes Les nombres suffisamment grands sont décomposables en sommes d'au plus 16 puissances quatrièmes.	État des connaissances g(n) = 19 Tous les nombres sont sommes au plus de 19 puissances quatrièmes de nombres entiers. G(n) = 16 Tous les nombres supérieurs à une certaine limite sont somme d'au plus 16 puissances quatrièmes de nombres positifs.
Les six nombres qui nécessitent plus de (16) termes. Le nombre 79 est le seul a nécessiter 19 termes. Le nombre 76 est le dernier à nécessiter 16 termes. Ce qui veut dira qu'au-delà de 79, la partition en puissances de 4 nécessite moins de 16 termes.	(17) 47 = 2 × 2^4 + 15 × 1^4 (17) 62 = 3 × 2^4 + 14 × 1^4 (18) 63 = 3 × 2^4 + 15 × 1^4 (17) 77 = 4 × 2^4 + 13 × 1^4 (18) 78 = 4 × 2^4 + 14 × 1^4 (19) 79 = 4 × 2^4 + 15 × 1^4
4P4 Il est classique de s'intéresser aux partitions des nombres en quatre puissances quatrièmes. Les nombres peuvent être répétés ou distincts. Et aussi, trouver une puissance quatrième décomposable en quatre puissances cinquièmes.	635 318 657 = 59^4 + 158^4 = 133^4 + 134^4 Trouvé par Euler en 1772

Tables des kP4 avec k nombres			haut
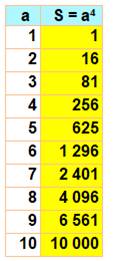
P4		0, 1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000, 14641, 20736, 28561, 38416, 50625, 65536, 83521, 104976, 130321, 160000, 194481, 234256, 279841, 331776, 390625, 456976, 531441, 614656, 707281, 810000, 923521, 1048576, 1185921, 1336336, 1500625, 1679616, 1874161, 2085136, 2313441, 2560000, 2825761, 3111696, 3418801, 3748096, 4100625, 4477456, 4879681, 5308416, 5764801, 6250000… OEIS A000583
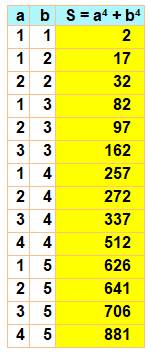
2P4		2, 17, 32, 82, 97, 162, 257, 272, 337, 512, 626, 641, 706, 881, 1250, 1297, 1312, 1377, 1552, 1921, 2402, 2417, 2482, 2592, 2657, 3026, 3697, 4097, 4112, 4177, 4352, 4721, 4802, 5392, 6497, 6562, 6577, 6642, 6817, 7186, 7857, 8192, 8962, 10001, 10016, 10081, 10256, 10625, 10657, 11296, 12401, 13122, 14096, 14642, 14657, 14722, 14897, 15266, 15937, 16561, 17042, 18737, 20000, 20737, 20752, 20817, 20992, 21202, 21361, 22032, 23137, 24641, 24832, 27297, 28562, 28577, 28642, 28817, 29186, 29282, 29857, 30736, 30962, 32657, 35122, 35377, 38417, 38432, 38497, 38561, 38672, 39041, 39712, 40817, 41472, 42512, 43202, 44977, 48416, 49297, 50626, 50641, 50706, 50881, 51250, 51921, 53026, 53057, 54721, 57122, 57186, 59152, 60625, 65266, 65537, 65552, 65617, 65792, 66161, 66832, 66977, 67937, 69632, 71361, 72097, 75536, 76832, 79186, 80177, 83522, 83537, 83602, 83777, 84146, 84817, 85922, 86272, 87617, 89041, 90082, 93521, 94097, 98162, … OEIS A003336
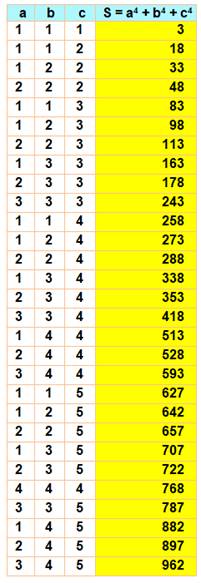
3P4		3, 18, 33, 48, 83, 98, 113, 163, 178, 243, 258, 273, 288, 338, 353, 418, 513, 528, 593, 627, 642, 657, 707, 722, 768, 787, 882, 897, 962, 1137, 1251, 1266, 1298, 1313, 1328, 1331, 1378, 1393, 1458, 1506, 1553, 1568, 1633, 1808, 1875, 1922, 1937, 2002, 2177, 2403, 2418, 2433, 2483, 2498, 2546, 2563, 2593, 2608, 2658, 2673, 2738, 2848, 2913, 3027, 3042, 3107, 3217, 3282, 3651, 3698, 3713, 3778, 3888, 3953, 4098, 4113, 4128, 4178, 4193, 4258, 4322, 4353, 4368, 4433, 4608, 4722, 4737, 4802, 4803, 4818, 4883, 4977, 4993, 5058, 5346, 5393, 5408, 5427, 5473, 5648, 6017, 6098, 6498, 6513, 6563, 6578, 6593, 6643, 6658, 6688, 6723, 6753, 6818, 6833, 6898, 7073, 7122, 7187, 7202, 7203, 7267, 7442, 7793, 7811, 7858, 7873, 7938, 8113, 8193, 8208, 8273, 8448, 8482, 8817, 8898, 8963, 8978, 9043, 9153, 9218, 9488, 9587, 10002, 10017, 10032, 10082, 10097, 10162, 10257, 10258, 10272, 10337, 10512, 10593, 10626, 10641, 10658, 10673, 10706, 10738, 10881, 10913, 11250, … OEIS A003337

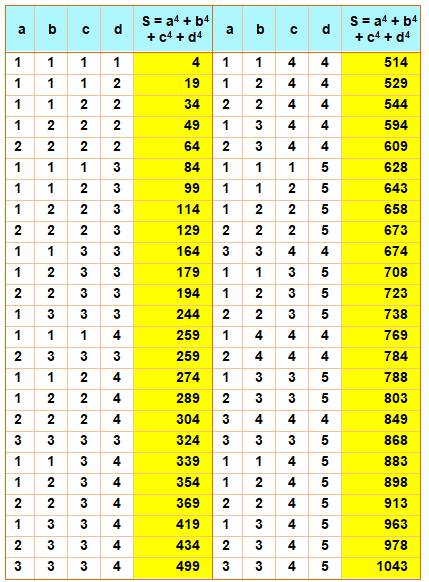
4P4

4, 19, 34, 49, 64, 84, 99, 114, 129, 164, 179, 194, 244, 259, 274, 289, 304, 324, 339, 354, 369, 419, 434, 499, 514, 529, 544, 594, 609, 628, 643, 658, 673, 674, 708, 723, 738, 769, 784, 788, 803, 849, 868, 883, 898, 913, 963, 978, 1024, 1043, 1138, 1153, 1218, 1252, 1267, 1282, 1299, 1314, 1329, 1332, 1344, 1347, 1379, 1393, 1394, 1409, 1412, 1459, 1474, 1507, 1522, 1539, 1554, 1569, 1584, 1587, 1634, 1649, 1714, 1762, 1809, 1824, 1876, 1889, 1891, 1923, 1938, 1953, 1956, 2003, 2018, 2064, 2083, 2131, 2178, 2193, 2258, 2404, 2419, 2433, 2434, 2449, 2484, 2499, 2500, 2514, 2547, 2562, 2564, 2579, 2594, 2609, 2624, 2627, 2644, 2659, 2674, 2689, 2739, 2754, 2802, 2819, 2849, 2864, 2914, 2929, 2994, 3028, 3043, 3058, 3104, 3108, 3123, 3169, 3171, 3188, 3218, 3233, 3283, 3298, 3363, 3473, 3538, 3652, 3667, 3699, 3714, 3729, 3732, 3779, 3794, 3842, 3859, 3889, 3904, 3907, 3954, 3969, 4034, 4099, 4114, 4129, 4144, 4179, 4194, 4209, 4259, 4274, 4276, 4323, 4338, 4339, 4354, 4369, 4384, 4403, 4434, 4449, 4513, 4514, 4578, 4609, 4624, 4689, 4723, 4738, 4753, 4803, 4804, 4818, 4819, 4834, 4864, 4883, 4884, 4899, 4947, 4964, 4978, 4993, 4994, … OEIS A003338

Carrés = somme de P4		haut
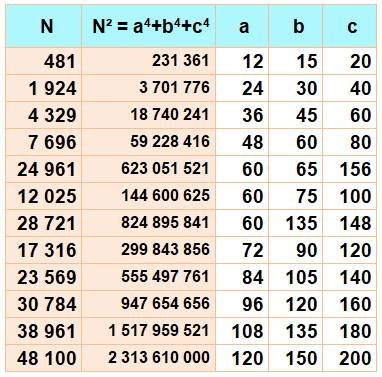
	481, 1924, 4329, 7696, 12025, 17316, 23569, 24961, 28721, 30784, 38961, 48100, 58201, 65441, 69121, 69264, 81289, 94276, 99844, 108225, 113241, 114884, 123136, 139009, 155844, 173641, 192400, 212121, 224649, 232804, 254449, 258489, 261764, 276484, 277056, 300625, 325156, 345761, 350649, 362401, 377104, 384161, 399376, 404521, 432900, 452964, 459536, 462241, 492544, 523809, 530881, 556036, 588969, 589225, 620321, 622089, 623376, 624025, 658489, 694564, 718025, 731601, 769600, 808561, 848484, 854401, 882889, 889369, 898596, 909321, 931216, 974025, 1017796, 1019169, 1033956, 1047056, 1062529, 1094481, 1108224, 1154881, 1163249, 1202500, … OEIS A365657 Notez que: les nombres de rang pair (comme 1924, 7696, ..) sont égaux à quatre fois un terme inférieur de la liste. Il semble que: les nombres a et c soient toujours pairs. Quant au nombre b, il serait impair une fois sur deux.

Sommes de rationnels

On peut étendre les recherches de sommes de puissances quatrièmes aux fractions. Ces solutions sont évidemment très difficiles à trouver.

Exemple

Somme deux fois en P4			haut
Deux termes Le plus petit nombre deux fois somme de deux puissances quatrièmes. Notez que l'on ne sait pas si une telle solution existe pour la puissance cinquième.	635 318 657 = 134^4 + 133^4 =158^4 + 59^4
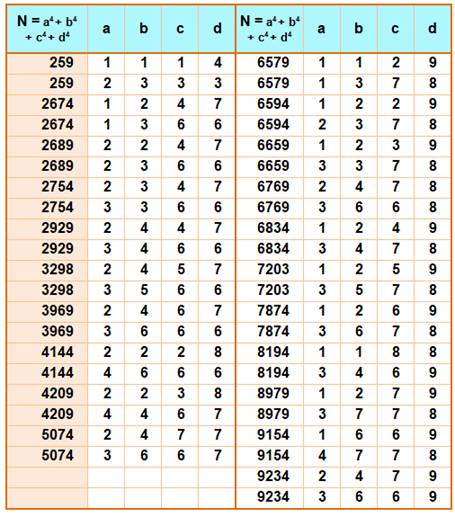
Deux fois quatre termes		259, 2674, 2689, 2754, 2929, 3298, 3969, 4144, 4209, 5074, 6579, 6594, 6659, 6769, 6834, 7203, 7874, 8194, 8979, 9154, 9234, 10113, 10674, 11298, 12673, 12913, 13139, 14674, 14689, 14754, 16563, 16578, 16643, 16818, 17187, 17234, 17299, 17314, 17858, 18963, 19699, 20658, 20739, 20979, 21154, 21219, 21329, 21363, 23123, 23409, 25554, 26562, 27314, 28594, 28609, 28674, 28849, 29218, 29443, 29889, 29954, 30738, 30994, 31203, 31234, 31409, 31474, 32689, 33379, 35139, 35154, 35379, 35394, 35459, 35634, 36003, 36674, 36754, 37298, 37378, 37779, 38593, 39073, 39298, 39474, 39729, 40849, 41089, 41939, 42194, 42738, 42769, 42784, 42849, 43024, 43219, 43234, 43299, 43393, 43474, 43843, 43889, 44064, 44514, 44994, 45123, 45169, 45378, 45619, 46274, 46864, 47314, 47379, 49329, 49779, 50019, …

Curiosité	haut
An On

Haut de page (ou double-clic)

Suite	Somme de 4 carrés Théorème de Lagrange S'y retrouver – Index Théorème de Waring Sommes des puissances cinquièmes de 1 à n Sommes des puissances de 5 de k = 1 à n Puissance 5 magique
Voir	Bi, tripartitions Carré des triangulaires = somme de cubes Cubes Nombre = sommes de cubes Nombre = sommes de puissances Nombres carrés Nombres cubes Nombres polygones Nombres triangles Puissances quatrièmes (bicarrés) Puissance = somme de puissances Table des puissances des nombres Somme multi puissantes Unité des puissances
Sites	Waring's problem – Wolfram MathWorld Conjecture d'Euler – Wikipédia Integers that are not the sum of positive powers – Brennan Benfield and Oliver Lippard – 2024
Cette page	http://villemin.gerard.free.fr/aMaths/Partition/SomP4.htm