|
Édition du: 15/06/2023 |
|
INDEX |
Jeux de Nombres avec grilles |
|||
![]()
|
TECTONIC Jeux de
grilles consistant à placer les nombres de 1 à 5 dans une grille partagée en
zones sans qu'un nombre ne se retrouve à proximité de lui-même. Ce jeu de
grille avec chiffres est notamment publié par le magazine hebdomadaire
Express. Ce jeu
est aussi connu sous les noms: SUGURU ou KEMARU® Une idée
pour chercher les solutions: copier la grille dans un traitement de texte.
Remplir toutes les cases vides avec la liste 12345 et supprimer
progressivement les chiffres impossibles. |
||
|
|
Sommaire de cette page >>> Débutant >>> Un exemple complet >>> Difficile >>> Suguru – Historique >>> Tectonic et pentaminos >>> Anglais |
Débutants Glossaire |
Exemple
de grille
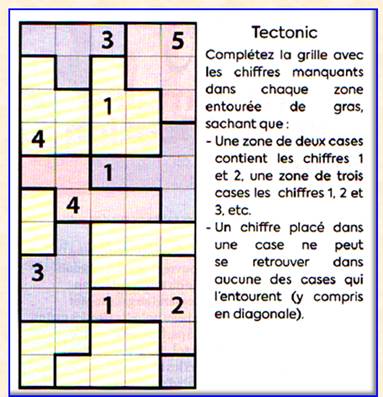
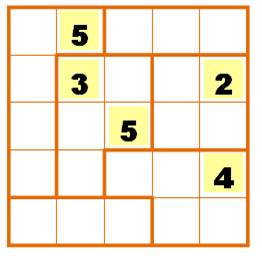
Publié par L'Express le 23 septembre 2021
|
Sur cette
grille 5x5, les traits épais délimitent des zones
de 1 à 5 carrés adjacents. Chacune des
zones doit contenir les nombres de 1 à 5 selon sa taille. Par exemple (1, 2
et 3) pour une zone à trois cellules. Deux
chiffres identiques ne sont jamais voisins, d'aucune façon. |
|
|
|
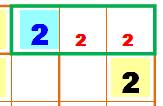
Étape 1 La zone
verte contient les nombre (1, 2 et 3). La
présence du 2 (jaune) interdit ce nombre dans les deux cellules juste
au-dessus (rouge). C'est la
cellule bleue qui contient le 2. |
|
|
|
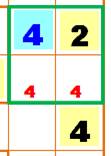
Étape 2 En jaune,
les nombres déjà placés. La zone
verte contient les nombres (1, 2, 3 et 4). La
présence du 4 en dessous interdit ce nombre dans les deux cellules inférieures
de la zone verte. C'est la
cellule bleue qui contient le 4. |
|
|
|
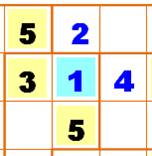
Étape 3 La
cellule bleue est entourée des nombres (2, 3, 4 et 5 C'est
donc qu'elle contient le 1. |
|
|
|
Étape 4 – Élimination par
double-cellule Les deux
cellules encadrées de vert contiennent le 1 et 3, dans un ordre ou l'autre. Toujours
est-il qu'elles interdisent ces deux valeurs dans la cellule bleue, en bas. Or, la
proximité du 4 et du 5, éliminent aussi ces valeurs. La seule
valeur possible pour la cellule bleue est le 2. On en
profite pour renseigner les cellules avec les nombres acceptables en gris. |
|
|
Étape 5 – Élimination par
triple-cellule La zone
verte contient les nombre (1, 2 et 3). L'une des
trois cellules contient un 2 qui interdit la présence du 2 dans la cellule
bleue inférieure. Or, on
sait que cette cellule contient le 2 ou le 4. Ce sera donc le 4 et le 2 sera
au dessus. Attention: cette zone verte influence la cellule centrale
en haut et pas du tout les deux cellules latérales. On ne peut pas dire que
la cellule 134 ne contient pas le 1 et le 3 et que par conséquent ce serait
le 4. |
|
|
Étape 6 – Régularisation Remarque: les plus aguerris auront vu qu'il était
possible de traiter la zone en haut à droite plus vite. On a simplement voulu
mettre en évidence les deux règles vues ci-dessus. Vous remplirez
les quatre cellules bleues sans difficulté compte tenu de la présence du 1. Le 1 vert
vous sera également simple à déduire. En
cascade, on en déduit les trois valeurs en ocre. |
|
|
Étape 7 – Finale Le 5 bleu
est imposé par le 1 et le 3 voisin. Suit automatiquement le 3 bleu. Pour les
cellules vertes, c'est le 2 voisin qui impose le 2 en haut. Le 3 voisin
impose le 3 en bas. Les deux
derniers (1 et 4) suivent automatiquement. |
|
Merci à Gilles Mevel
|
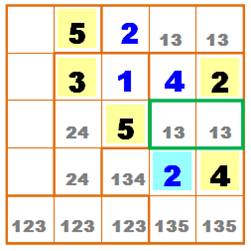
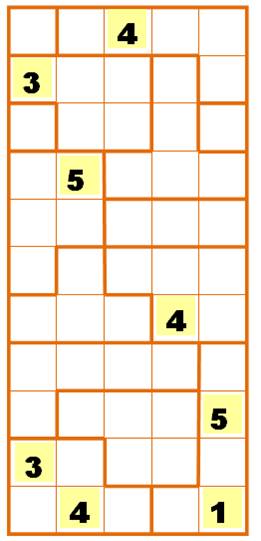
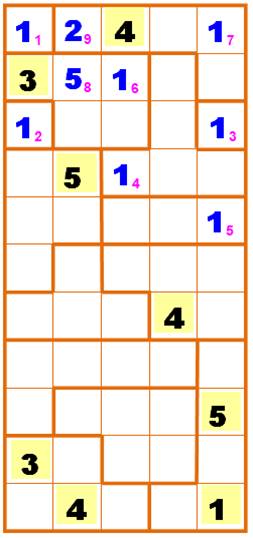
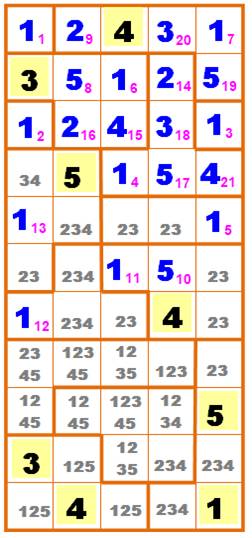
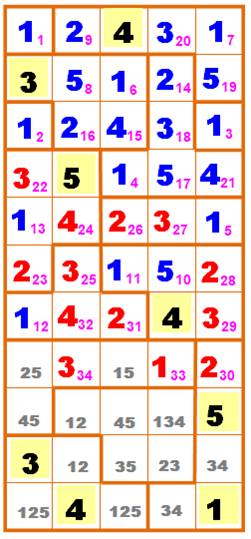
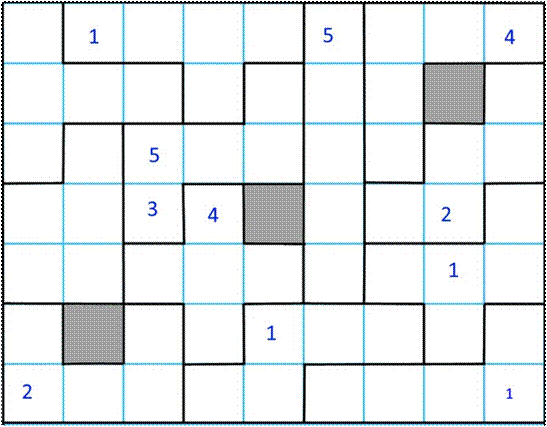
À gauche, la grille de
départ avec huit nombres placés. La grille de droite montre les cellules que l'on
peut remplir facilement. Les zones à une seule case contiennent un 1. On
commence par celles-là. Les remplissages successifs sont numérotés par un
indice en rose. De 1 à 9 Cellule unique avec un 1 en 11, 12
et 13. Le 14 résulte du 13.
Lequel, avec 12, entraine 16
puis le 17. Le 58 résulte du 5 jaune plus bas. Le 29 profite d'une configuration propice car il est entouré de tous
les autres chiffres. |
|
|
|
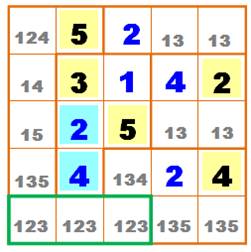
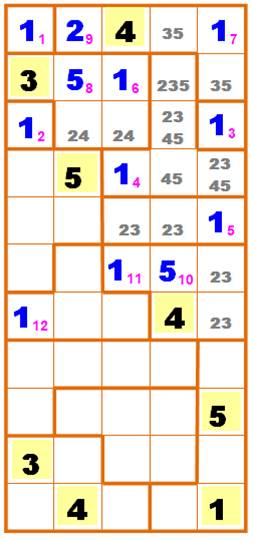
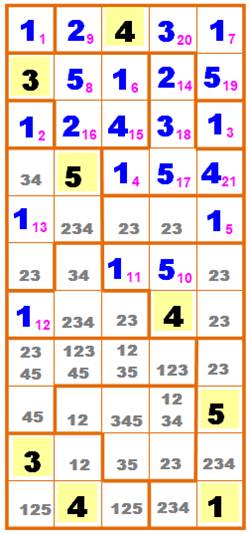
En gris, on indique les chiffres possibles dans
les cellules. Par exemple: les deux 35 en haut à droite, exclut
le 35 dans la cellule d'angle. Ce qui impose le 214. De même dans la zone à trois cellules au milieu,
donne deux fois 23 qui encore exclut les 2 et 3 dans les cellules du milieu
en haut et en bas. Notamment, le 4 placé et le 15, impose
le 510. On en déduit 111
et 112. |
|
|
|
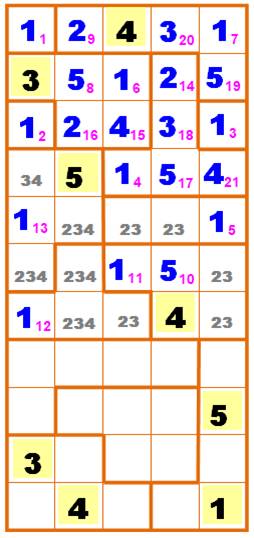
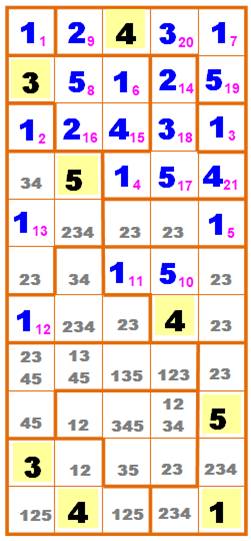
Trois étapes suivantes qui agissent sur les propriétés
du remplissage. Observez comment dans l'équerre juste en dessous du 112,
la présence du 4 trois fois élimine le 4 dans la cellule embrassée. C'est
aussi le cas avec le 5 qui élimine le 5 dans au même endroit. Il y reste
seulement le 12.
|
||
|
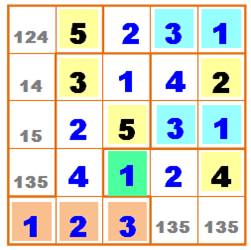
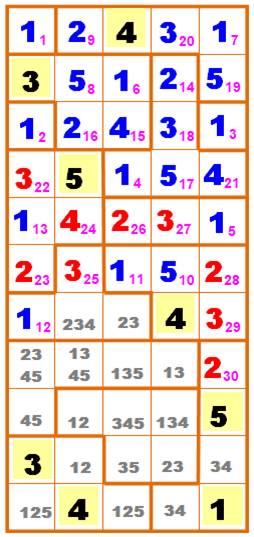
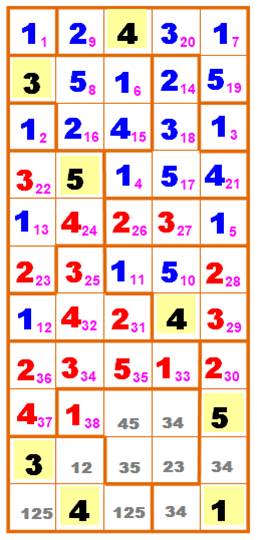
Rien d'une logique simple ne se présente ici. La
tactique consiste à tester une valeur et de vérifier la validité jusqu'au
bout. Dans la colonne de gauche, on choisit 322 qui offre une
simple alternative avec le 4. Chiffres nouveaux en rouge.
|
||
|
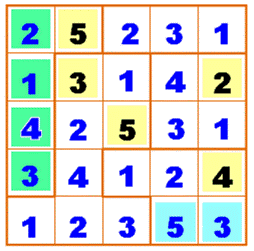
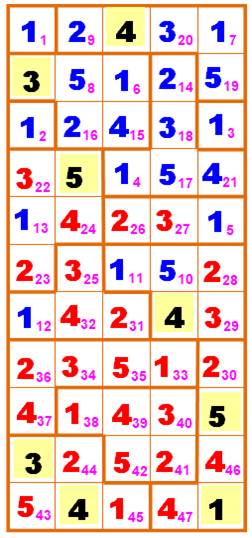
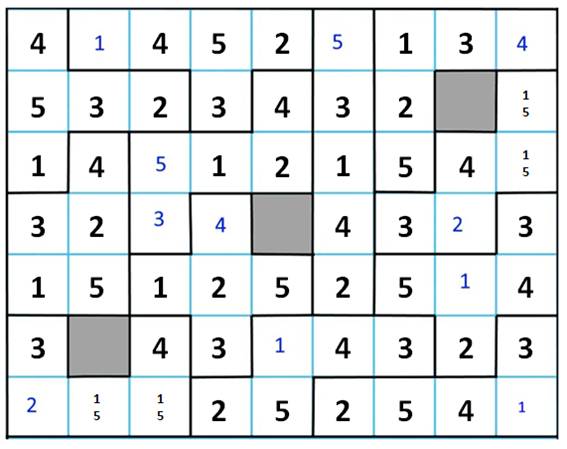
Le choix du 322 fut bon, car on
atteint le remplissage complet sans contradiction. À droite, la solution sans les indices de
progression. Note: avec 422, on trouve également au
moins une solution valide. Ce qui laisse penser que ces énigmes offrent
plusieurs possibilités de solutions. |
|
|
|
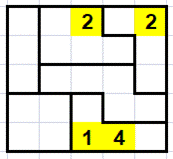
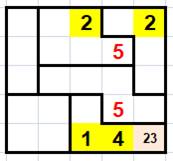
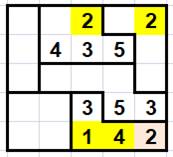
Une
grille 5x5 avec seulement quatre nombres placés. Avec si
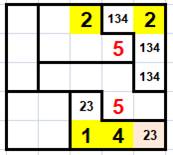
peu de données, la résolution de cette grille ne semble pas facile. Les deux 5 rouges sont placés du fait des
exclusions par les équerres. |
|
|
|
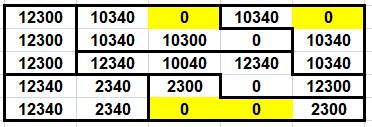
Le tableau des
présences montre les possibilités pour chaque cellule. 12300 veut dire que l'on peut y placer le 1, 2 ou
le 3; en revanche, 4 et 5 sont exclus. Le 0 seul indique que la cellule est résolue. |
|
|
Tableur
|
Il
est assez facile de créer un outil d'aide à l'établissement du tableau des
présences. La notation adoptée permet de faire les calculs logiques. Ma
méthode: on crée cinq tableaux: chacun montrant les exclusions du 1, du 2 …
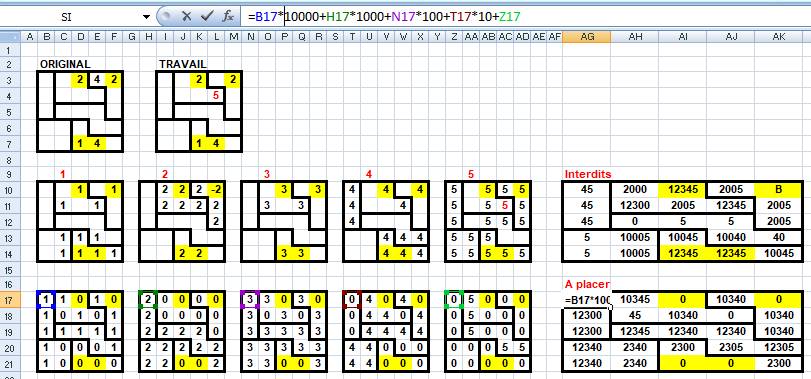
du 5. Pour
établir le tableau des présences, on calcule un nombre pour chaque cellule,
lequel reprend les positions vides, pondérées par une puissance de 10. Exemple de disposition et de formule de calcul
Les
tableaux du bas indiquent les possibilités. Ils sont calculés automatiquement
à partir des tableaux du milieu: lesquels indiquent les exclusions et sont
remplis à la main. |
Voir Tableur
|
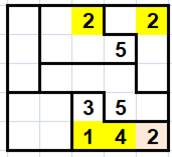
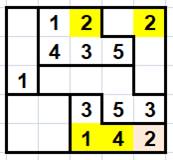
La suite de la résolution de la grille est plus
coriace ! Ma tactique, choisir une valeur et tester la
suite. Avec 3, en bas à droite, on arrive rapidement à une impasse. En choisissant
le 2, on termine la grille sans trop de difficultés. |
|
|
|
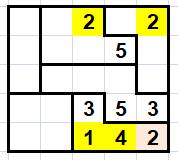
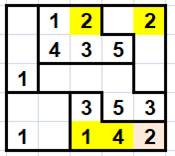
Étapes intermédiaires. On met à jour le tableau des présences au fur et à mesure des nombres
trouvés. |
|
|
|
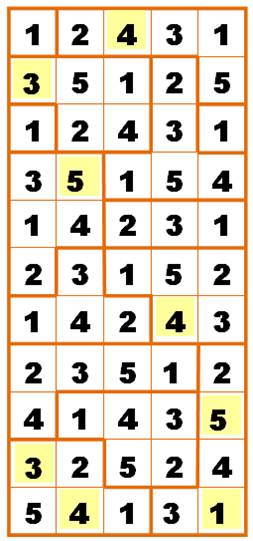
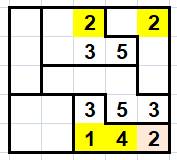
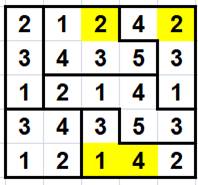
Solution |
|
|
|
Grille à compléter Les zones
élémentaires sont formées des douze pentaminos
Solution
Sur une idée de
Jean-Jacques Lelez. Cette grille est de sa composition Merci pour m'avoir communiqué ce jeu |
|
|
Inaba propose ses jeux en lignes,
mais en Japonais. Il est publié dans les journaux américains: New York Times
été The Guardian. Sarah Caster en présente une
sélection sur son site (M+A+T+ = LOVE) destiné à l'enseignement La version Romaji du nom japonais de
ce puzzle est Nanba Burokku, qui se traduit littéralement par " blocs de
chiffres ". Estimant que cette traduction ne reflétait pas suffisamment
les qualités de ce puzzle, nous l'avons rebaptisé Suguru (signifiant "
groupes de chiffres " et, par coïncidence, un nom de garçon japonais). Suguru est, selon nous, un puzzle
sublime, avec des règles encore plus simples que celles du Sudoku et un défi
de logique pure plus impliqué et plus satisfaisant. |
Selon
le magazine PUZZLER
|
A
grid of cells is divided into outlined blocks containing up to five cells.
Each cell in an outlined block contains a digit from 1 to n (where n is the
number of cells in that block). So,
a single-cell block contains the digit 1, a block of two cells contains the
digits 1 and 2, and so on. The
aim is to fill the grid so that no same digit is touching, not even
diagonally. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |