|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
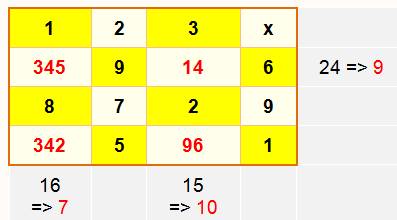
KAKURO – Exemple DÉBUTANT Un exemple résolu pas à pas. Suite à questions d'internautes. Légèrement différent du Kakuro traditionnel. Retour à l' Introduction |
Anglais:
cross sum puzzles
|
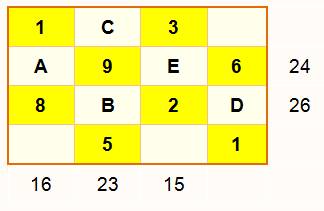
Problème |
|
|
|
|
|
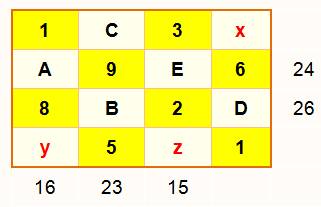
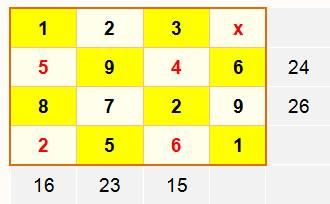
Étape 1 |
|
|
|
|
|
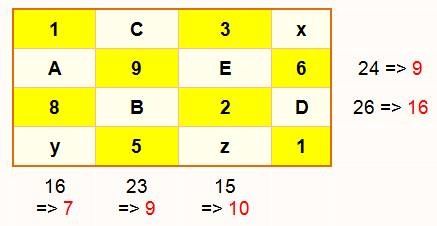
Étape 2 |
|
|
|
|
|
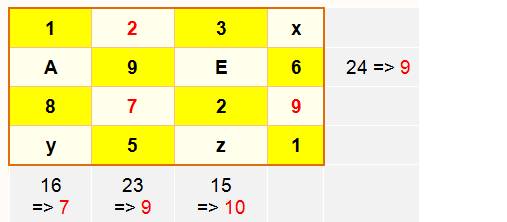
Étape 3 |
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()