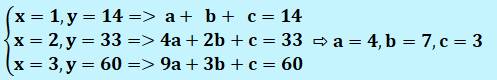|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SPIRALE d'Ulam Curiosités La
spirale des nombres, proposée par Ulam en 1963, amuse toujours les
chercheurs, amateurs ou professionnels. Cette
page indique quelques pistes de recherche. Rappel: pour
isoler les nombres premiers,
l'organisation en roue de 30 rayons reste la
disposition la plus riche. Ici,
les nombres composés
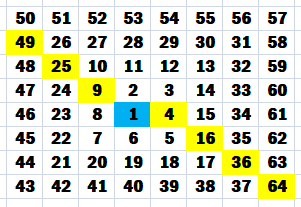
sont à la fête. Existe-il des alignements de nombres tous composés dans la spirale d'Ulam ? Oui ! |
Anglais: Ulam Spiral, prime spiral
|
|
||
|
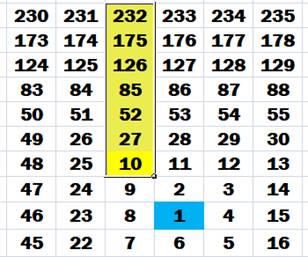
Tous les
nombres au carré
sont situés sur la diagonale descendante. Le nombre
1 est sur la couronne 0 (celle du nombre 1), le 2 sur la couronne 1, etc.
Tous ces
nombres sont composés. |
|
|
|
|
||
|
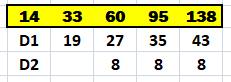
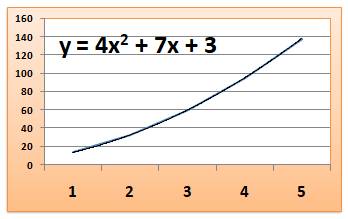
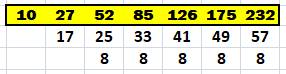
Mise en équation Choisissons
la ligne: 14, 33, 60, … Calcul
des différences premières et secondes:
La
différence seconde est constante, un polynôme du second degré convient: Avec
trois points de référence, on trouve: Conclusion Toutes les
valeurs sur cette ligne sont le produit de deux nombres (x+1) et (4x+3). Ce
sont des nombres composés. |
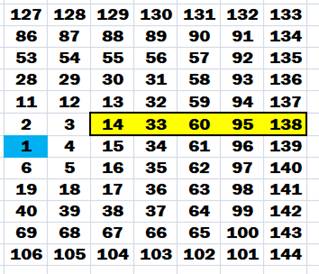
Tous les nombres de cette
demi-droite (jaune) sont composés jusqu'à l'infini.
|
|
Recherche de l'équation
|
Deux méthodes pour trouver les paramètres de
l'équation 1)
Résoudre le système d'équations
2)
Réaliser le graphe sur tableur et demander une courbe de tendance polynomiale de degré 2 et cocher afficher l'équation.
|
|
|
||
|
Mise en équation Différences
première et seconde:
Il s'agit
également d'un polynôme du second degré: y = 4x² + 5x + 1 = (x + 1) (4x + 1) Conclusion Toutes
les valeurs sur cette ligne sont le produit de deux nombres (x+1) et (4x+1).
Ce sont des nombres composés. |
Tous les nombres de cette
demi-droite (jaune) sont composés jusqu'à l'infini.
|
|
|
|
||
|
Toutes
les demi-droites contentant des nombres composés ont une équation en: |
Les nombres pairs, par nature, sont composés. On les trouve sur les obliques de la spirale
des nombres. Les nombres impairs sont susceptibles d'être premiers.
Il est pratique de constituer une spiral des nombres impairs pour
identifier des organisations particulières. |
|
|
Nombres pairs La valeur de y est
paire dès que a ou b est pair. Ces deux
exemples sont représentés par des lignes obliques sur la spirale des nombres. |
Exemples (sur toute cette colonne) y = (x + 2) (4x
+ 2) {18, 40, 70,
108, 154, 208, 270, 340, 418, 504, …} y = (x + 2) (4x
+ 4) {24, 48, 80,
120, 168, 224, 288, 360, 440, 528, ..} |
|
|
Nombres impairs composés La valeur de y
est impaire à condition que a et b soient tous deux impairs. |
y = (x + 1) (4x
+ 1) {10, 27, 52, 85,
126, 175, 232, 297, 370, 451, …} |
|
|
Nombres carrés Ils sont tous
sur la diagonale descendante. Voir Ci-dessus |
y = x² {1, 4, 9, 16,
25, 36, 49, 64, 81, 100, …} |
|
|
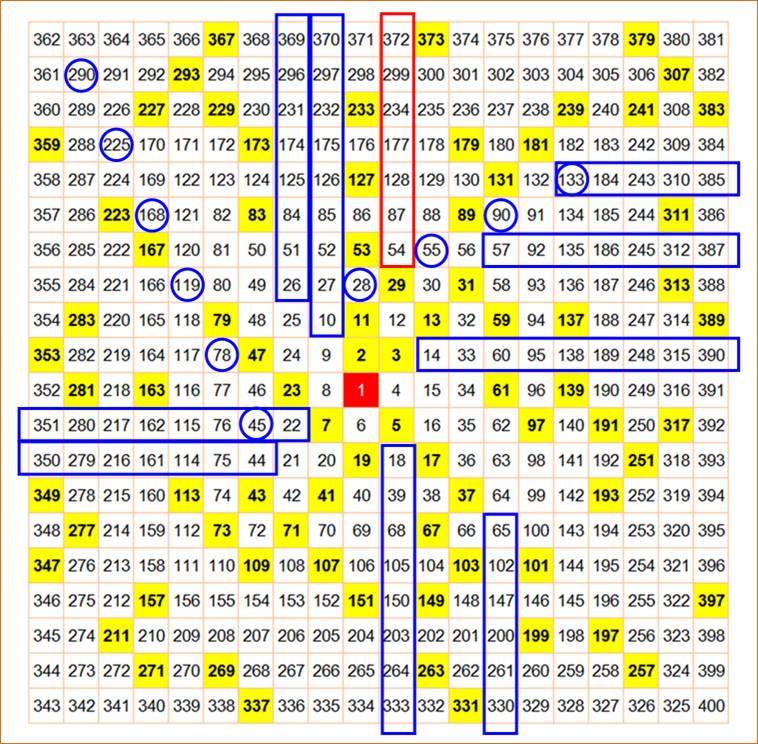
Autres diagonales La première
série ci-contre produit une demi-diagonale avec saut. La seconde débute
par une diagonale avec saut pour rejoindre une bande horizontale |
y = (x + 3) (4x
+ 1) (cercles bleus
sur la grille) {45, 78, 119,
168, 225, 290, 363, 444, 533, …} y = (x + 3) (4x
+ 3) (cercles puis bande) {28, 55, 90,
133, 184, 243, 310, 385, 468, 559, ..} |
|
|
Demi-droites pseudo-impaires Cette
demi-droite, par exemple, semble exempte de nombres premiers. C'est faux ! On va les
trouver plus loin: 857, 2837 … |
y = 4x² + 5x + 3
(bande rouge sur la grille) {12, 29, 54, 87,
128, 177, 234, 299, 372, 453, ..} |
|
|
Autres Toutes les
fonctions y = (x + a ) (4x + b) ne sont pas pertinentes sur la spirale (par
de forme intéressnte), même si elles ne produisent que des nombres composés |
y = (x + 5) (4x
+ 1) {30, 63, 104,
153, 210, 275, 348, 429, 518, 615, …} |
|
|
À l'origine, la
spirale des nombres a été utilisée dans le but de repérer des alignements
particuliers de nombres premiers. Ces alignements,
traduits en formules, fournissent plus ou moins de nombres premiers. Il est aussi
possible, par curiosité, de repérer des alignements qui eux produisent des
nombres composés. Ces alignements
existent, mais ne permettent pas de nettoyer la grille de façon à isoler les
nombres premiers. A contrario, la roue des nombres premiers, isole parfaitement les nombres
premiers et rétrécit grandement le domaine de recherche de ces nombres
premiers. |
Merci à Olivier MEHAYE dont les indications m'ont permis de vérifier cette
page
Il propose de poursuivre les recherches en composant la spirale avec
les nombres impairs seulement ou les pairs..
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()