NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/01/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	ORDRE géométrique				Glossaire Nombres Premiers
INDEX Nombres premiers – ORDRE	Cribles (types)		Crible d'Ératosthène	Crible de Sundaram
	Tableaux		Cercles et croix	Crible de la roue
	Spirales d'Ulam		Carrés magiques premiers	Crible d'Atkin
	Triangle de Klauber		Conjecture de Gilbreath	Méthode René Nève
		Sommaire de cette page >>> Crible de Sudaram >>> Alternative et explications

CRIBLE DE SUNDARAM

Critère de primalité, alternative au crible d'Ératosthène.

Sundaram, mathématicien indien, a publié ce crible en 1934.

Le principe est assez simple: lister tous les nombres impairs composés; les nombres absents sont des nombres premiers.

CRIBLE DE SUNDARAM

On forme le tableau illimité suivant dans lequel les lignes et les colonnes sont en progression arithmétique.

4	7	10	13	16	19	22	25	...
7	12	17	22	27	32	37	42
10	17	24	31	38	45	52	59
13	22	31	40	49	58	67	76
16	27	38	49	60	71	82	93
19	32	45	58	71	84	97	110
22	37	52	67	82	97	112	127
25	42	59	76	93	110	127	144
...

Propriété de Sundaram

Si N est dans ce tableau, Alors 2N + 1 n'est pas premier.

Si N n'est pas dans ce tableau, Alors 2N + 1 est premier.

Exemples pour N < 12

N	NTABLEAU	2N + 1	Premier	Composé
1		3	P
2		5	P
3		7	P
4	4	9		C
5		11	P
6		13	P
7	7	15		C
8		17	P
9		19	P
10	10	21		C
11		23	P
12	12	25		C

Alternative et explications
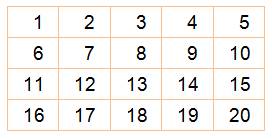
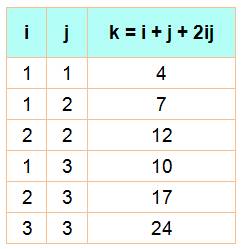
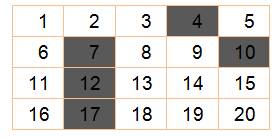
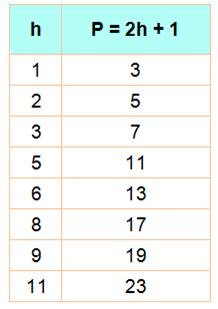
Liste des entiers de 1 à n Tous les nombres de la forme i + j + 2ij jusqu'à n sont retirés (i j). Les nombres qui subsistent sont doublés et incrémentés. Ce sont les nombres premiers impairs.

Principe de justification
Soit q un entier impair.	q = 2k + 1
Ce nombre est éliminé si k est le forme requise.	k = i + j + 2ij q = 2(i + j + 2ij) + 1
Mise en facteur	q = 2i + 2j + 4ij + 1 q = 2i(1 + 2j) + 1 + 2j q = (2i + 1) (2j + 1)
Les nombres exclus sont ceux qui se factorisent; tous ceux qui se factorisent.	(2i + 1) (2j + 1)
Les nombres qui subsistent sont:	premiers

Voir	Cribles Méthode de René Nève Nombres premiers en tableaux Barre magique Séquences en 6n Crible d' Ératosthène Nombres premiers – Index
Aussi	Liste de nombres premiers Types de cribles Crible de Moessner Ératosthène Facteurs premiers autour de 1000 Nombres composés Premiers en cercles et croix Programmation du crible d'Ératosthène Représentation des nombres Spirale d'Ulam
Site	Sieve of Sundaram – Wikipedia – Belle animation
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/sundaram.htm