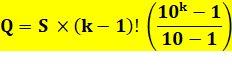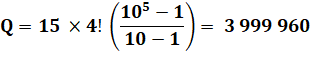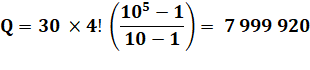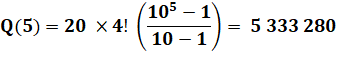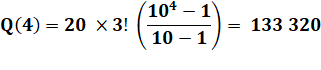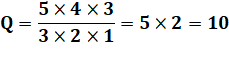|
Édition du: 10/12/2022 |
|
INDEX |
Avec les chiffres |
||
Faites un double-clic pour un retour en haut de page
![]()
|
avec chiffres sous contrainte Calcul de la
somme de tous les nombres de k nombres avec jeu de k nombres. Calcul de la
somme de tous les nombres formés avec un jeu donné de chiffres. Calcul de la somme
des nombres formés par permutation ou combinaison de ces chiffres. Trouver les permutations
conduisant à une somme donnée. |
||
|
|
Sommaire de cette page >>> Nombres à k nombres avec jeu de k nombres >>> Nombres à trois chiffres avec répétition >>> Nombres à trois chiffres sans répétition >>> Nombres à trois chiffres sans permutation >>> Programmation >>> Jeu de k nombres sous contrainte d'un total |
Débutants Glossaire |
|
Question Quelle est la somme de tous les nombres à k chiffres
formés avec un jeu de k chiffres. ? Le facteur final e 10 puissance est égal à un repunit
de k chiffres. Si k = 3, on a: 111. |
Réponse
Avec k chiffres et S leur somme. |
|
|
Exemple Nombres formés avec les chiffres 1, 2, 3, 4 et 5. |
|
|
|
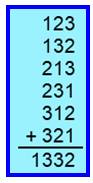
Table pour k chiffres de 1 à k Exemple avec k = 2, on a: 12 + 21 = 33 Exemple avec k =
3, on a: 123 + 132 + 213 + 231 + 312 + 321 = 1 332 |
|
|
|
Jeu
de nombres quelconques {2, 4, 6, 8, 10} |
|
|
|
Cas du 0 {0,
2, 4, 6, 8} Les nombres commençant par 0, donc nombres à quatre chiffres, doivent être
retranchés. |
|
|
Voir Brève
48-946
|
Nombres à trois chiffres sans permutation dans un jeu de cinq chiffres |
||||
|
Question Nombres à trois chiffres formés avec les seuls chiffres
1, 2, 3, 4 et 5. Combien ? Quelle est leur somme ? |
Réponse Il y a 10 tels nombres Somme: 1 845 |
|||
|
Quantité Il s'agit de choisir trois chiffres parmi cinq
disponibles: cinq choix pour le premier nombre, quatre pour les deuxième et
trois pour le troisième; soit: A diviser par 6 pour éliminer les permutations; Q = 60 / 6 = 10 |
Les 10 nombres 123, 124,
125, 134, 135, 145, 234, 235, 245, 345. La
quantité est en fait la quantité de combinaisons
de 3 parmi 5 qui se calcule:
|
|||
|
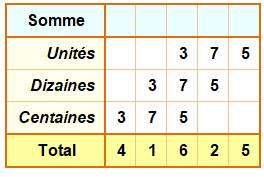
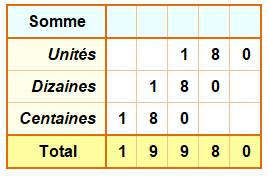
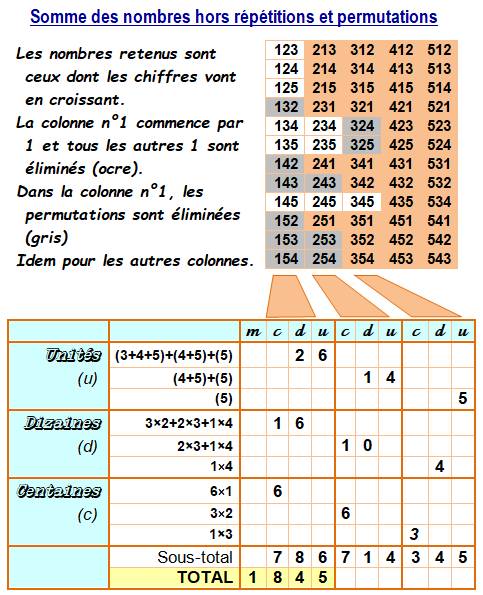
Somme (S) Avec si peu de nombres, on peut effectuer la
somme de ces dix nombres: 1 845. Si l'on recherche un algorithme, les choses se compliquent. En tout cas, ce n'est pas six fois moins que le cas
avec permutations. Le tableau montre une disposition du calcul qui
montre les dénombrements et calculs pour chaque chiffre des unités, dizaines
et centaines. Il se dessine une certaine logique. Et, il sera possible d'encapsuler ce tableau en
une formule. Mais, elle sera compliquée pour le cas général d'un nombre à k
chiffres par un jeu de n chiffres donnés.
|
|
|||
|
|
But Calculer la somme des combinaisons et des
permutations. Commentaire Appel des logiciels de combinatoire (combinat). Procédure qui restitue les nombres à partir de
leurs chiffres et calcule leur somme. Ces nombres sont obtenus en formant une liste des
combinaisons (choose) ou une liste de
permutations (permute). Exemple de liste pour
choose (5, 3):
|
|
Voir Programmation – Index
|
Question Avec un jeu donné de nombres, trouver les
combinaisons dont la somme vaut un total fixé, chaque nombre est utilisé une
seule fois (combination sum problem). Solution Pas de solution simple. Même ! Le problème
est NP complet (c.a.d: très difficile, même avec un ordinateur). Ce problème est du même style que le problème du sac à
dos) ou encore celui de la somme à payer avec
diverses pièces (the coin changing problem). Objet de nombreux exercices de programmation sur
Internet. |
Exemples Chiffres: {1, 2, 3, 4, 5} Somme: 357 Solution: 123 + 234 = 357 Chiffres: {1, 2, 3} Somme: 56 Solution: 12 + 23 + 21 = 56 Chiffres: {3, 9, 8, 4, 5, 7, 10} Somme: 15 Solutions: [5, 10], [7, 8], [3, 5, 7], [3, 8, 4] |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |