|
||||||||||||||||||||||||||||
![]()
|
Facteurs sans présence du 0 Parmi tous les produits
possibles pour atteindre un nombre, lesquels ne comportent aucun 0. Pour les puissances de 10, ces
nombres sont extrêmement rares. |
|
|
|||||||||||||||
|
Produit
dont chacun des deux facteurs ne comporte pas de zéro.
Le
produit 4 x 25 est le seul éligible, ne comportant pas le chiffre zéro. |
|||||||||||||||
|
On
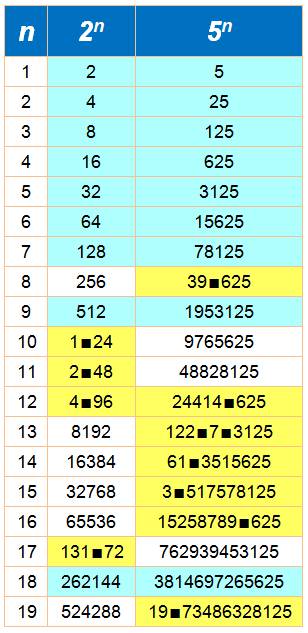
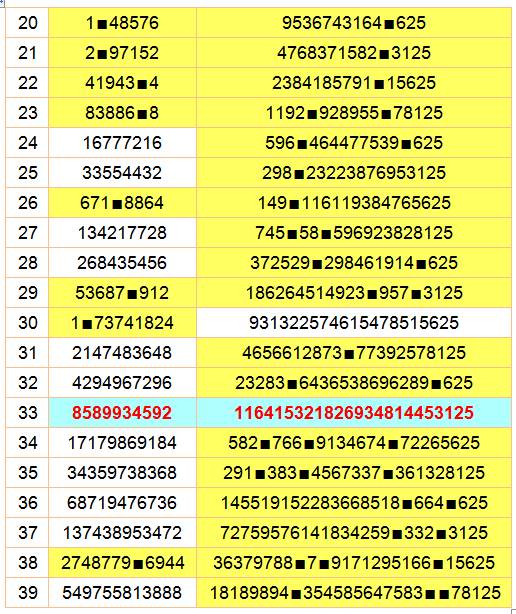
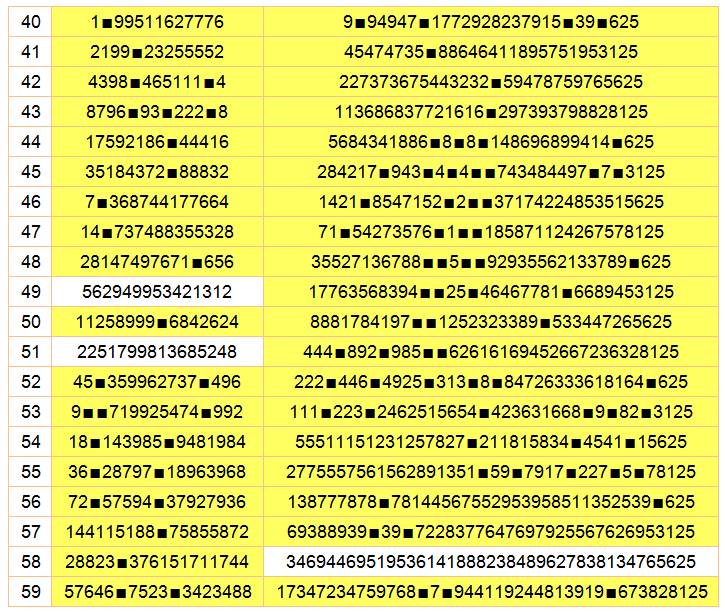
ne conserve que la configuration éligible: 10n = 2n . 5n Pour
mieux les visualiser les 0 dans le tableau, ils sont marqués La
ligne complète en bleue donne les 10n dont un des produits ne
contient pas de zéro. Parfait
jusqu'à 107. Très rare par la suite. Dans
cette analyse jusqu’à 10100 , la plus
grande puissance de 10 ayant un produit sans zéro est 1033. Il y en a 10 au
total dans ce tableau. C’est sans doute un résultat vrai pour tout n
jusqu’à l’infini. J’ai moi même testé qu'il n’y a pas de puissance
de 2 sans zéro jusqu’à 10500.
|
|
|
|
|
|
Exemple avec Maple for i from 1 to 100 do lprint (i, 2^i, 5^i): od;
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()