NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/01/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Géométrie
Débutants Géométrie	Démonstration		Glossaire Géométrie
INDEX Géométrie Enseignement	Débutant	Angle au centre
	Cinquième	Sommaire de cette page >>> Étapes de la démonstration >>> Exemple 1 >>> Exemple 2

Démonstration en géométrie

Comment s'y prendre pour poser une démonstration, notamment en géométrie? Cette page est destinée aux élèves de collèges dès qu'ils abordent les mathématiques un peu plus abstraites.

La géométrie est comme un jeu de construction qui élabore des conclusions à partir des données du problème (énoncé) et des connaissances déjà acquises (théorèmes).

Étapes
Rédaction Supposons le problème résolu, il faut alors le rédiger. L'espace de rédaction est divisé en quatre grandes parties: Données: le rappel des informations importantes de l'énoncé, y compris le fameux: "ce qu'il faut démonter"; Théorèmes: l'énoncé des théorèmes qui seront utilisés dans le cœur de la démonstration. C'est la boite à outils; Le cœur de la démonstration qui indiquera, ligne à ligne, une explication suivi d'une conclusion, d'une déduction; L'explication s'appuie sur: les données connues, les théorèmes annoncés, et les conclusions déjà obtenues au cours de cette démonstration. La dernière conclusion clôt la démonstration		La rédaction d'une démonstration est structurée en quatre grandes parties. Les deux premières constituent le point de départ: c'est l'état des connaissances. Les deux dernières forment le cœur de la démonstration: c'est la partie raisonnement.
Recherche de la solution Quatre étapes fondamentales. Chacune a son importance. Les deux premières sont primordiales. Il faut leur donner du temps. Pendant ce temps le cerveau se met en activité en parcourant les parties du cours qui pourrait avoir de l'intérêt dans l'établissement de la solution. Note: nous sommes bien au niveau d'un devoir scolaire. Le professeur cherche à vous faire pratiquer le cours. Alors pensez d'abord à la leçon que vous venez d'apprendre.

Exemple 1
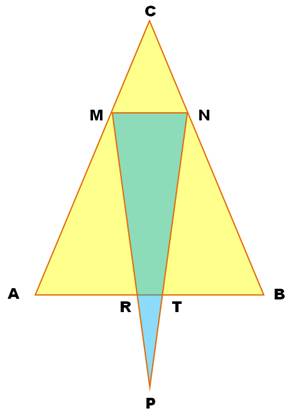
Énoncé Deux triangles isocèles ABC et MNP. Leurs bases AB et MN sont parallèles. Les points M et N sont situés sur les côtés AC et BC du triangle ABC. MP coupe AB en R et NP coupe AB en T. Démontrez que les angles AMR et BNT sont égaux. Ma réflexion Triangles isocèles égalité des côtés Bases parallèles avec une sécante, création d'angles égaux. La figure me montre que les angles AMR + RMN + NMC = 180°. Est-ce une piste? Ma rédaction:	Figure
Données ABC et MNP isocèles AB // MN Ce qu'il faut démontrer AMR = BNT	Théorèmes 1) Dans un triangle isocèle, les côtés autres que la base sont égaux. 2) Dans un triangle isocèle, les angles à la base sont égaux. 3) Une sécante et deux droites parallèles: les angles correspondants sont égaux
Explications	Conclusions
Le triangle ABC est isocèle; ses angles à la base sont égaux.	BAC = ABC		1
Les segments AB et MN sont parallèles, la sécante AC forment deux angles correspondants égaux.	BAC = NMC		2
Idem de l'autre côté.	ABC = MNC		3
En rapprochant des trois propriétés: 1, 2 et 3.	BAC = ABC NMC = MNC		4
Le triangle NMP est isocèle; ses angles à la base sont égaux.	RMN = TNM		5
Les angles en M et N s'ajoutent pour former des angles plats AMC et BNC	AMR + RMN + NMC = PNT + TNM + MNC = 180°		6
Des égalités 4 et 5, nous pouvons retrancher des quantités égales de chaque côté de l'égalité	AMR + RMN + NMC = NNT + TNM + MNC		7
C'est l'égalité qu'il fallait démontrer.	AMR = BNT
Note: L'énoncé donne des informations non nécessaires pour pigmenter l'exercice. Les points R et T sont inutiles. P aurait suffit. Présents, ces deux points parasites pourraient nous entrainer sur la piste de l'égalité des triangles AMR et BNT. Ce qui est une voie possible, par exemple, en démontrant que le triangle RTP est isocèle.

Suite	Démonstrations Angle au centre – Exemple de présentation de démonstration
Voir	Bases de la géométrie
Livre	Donc, d'après. Une construction axiomatique de la géométrie au collège – Philippe et Lauréline Colliard – Mathemagique.com – 2014
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/GEOMETRI/Demo1.htm