|
Édition du: 02/04/2024 |
|
INDEX |
Échecs – Cavalier |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
♞ PÉRIPLE du CAVALIER ♞ Historique, Théorie et
Programmation Le périple du cavalier sur
un échiquier classique a été étudié par de très nombreux savants et amateurs.
Euler, encore lui, fut un précurseur pour établir les lois de composition de
tels parcours. Ce problème du cavalier est un sujet classique de
l'apprentissage de la programmation. |
||
|
|
Sommaire de cette page >>> Théorie >>> Programmation >>> Historique |
Débutants Glossaire |
Anglais: The move of a
chess knight, knight's tour / The knight tour problem
Environnement
|
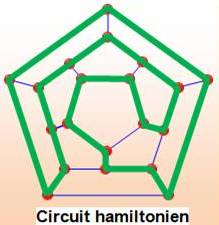
Le périple du cavalier fait partie des problèmes
de trajet hamiltonien sur un graphe:
chaque sommet est visité et cela une seule fois. Si le trajet est fermé, on a un cycle
hamiltonien. Alors c'est un problème semblable à celui du voyageur de
commerce. La résolution de ces problèmes est complexe, du
type NP-complet.
Cependant, le périple du cavalier peut être résolu en un temps linéaire. |
|
|
|
Directe, bestiale ou force-brute |
Analyse de chacune des possibilités pour chaque
case atteinte. Impossible dès que la taille de l'échiquier
augmente. |
|
|
Symétries |
Le processus peut être un peu accéléré en
cherchant unes solution symétrique en effectuant, pour chaque mouvement, les
mouvements symétriques et en essayant de les raccorder à la fin. |
|
|
Boucles |
Le procédé consiste à construire de petites boucles
et à les réunir. Pour cela on ouvre deux bouches à des endroits proches qui
peuvent se raccorder par deux mouvements de cavaliers. |
|
|
Algorithmes |
Plusieurs algorithmes permettent de minimiser les
recherches. Par exemple, tenir à jour la liste des cases non visitées qui
permettraient d'accéder à une case non visitée. |
|
|
Règle de Warndorf |
Le cavalier est déplacé de manière à se diriger
toujours vers la case à partir de laquelle il aura le moins de mouvements en
avant. Lors du calcul du nombre de déplacements en avant
pour chaque case candidate, nous ne comptons pas les déplacements qui
revisitent une case déjà visitée. Il est possible d'avoir deux choix ou plus pour
lesquels le nombre de coups en avant est égal ; il existe diverses méthodes
pour briser de tels liens, dont une conçue par Pohl et une autre par Squirrel
et Cull. Cette méthode heuristique est capable de trouver
une solution en temps linéaire. Un tel programme a été écrit par Gordon
Horsington et publié en 1984 dans le livre Century/Acorn User Book of
Computer Puzzles. |
|
|
Réseaux de neurones |
Tout mouvement possible est représenté par un
neurone. Chacun d'eux est initialisé au hasard dans une position active ou
inactive. En fonctionnement chacun des neurones réagit en
fonction de l'état de ses voisins et selon des règles programmées. En principe, le réseau converge vers une
solution. Ce qui est le cas lorsque, à une nouvelle étape, aucun des neurones
n'est amené à changer. |
|
|
Inde |
Première occurrence dans un traité d'ornement
poétique indien, le Kavyalankara du poète Rudrata. |
|
|
840 |
Al-Adli ar-Rumi donne une solution pour
l'échiquier 8×8. |
|
|
Xe siècle |
Parcours de l'intégralité d'un demi-échiquier de
32 cases a été trouvée dans un manuscrit en Inde |
|
|
1141 |
Quatre poèmes de 64 vers dont chacun est associé
aux coordonnées d'une case de l'échiquier connus dans le monde
arabo-musulman. |
|
|
XIVe siècle |
Manuscrit anglo-normand: parcours ouvert dont le
but est d'amener le cavalier d'un coin à un autre. |
|
|
XVIIe siècle |
Encyclopédie indienne: exemple de parcours fermé
sur un échiquier de 64 cases. Charles Monneron rapporte d'Inde une solution avec
départ et arrivée accolés |
|
|
XVIIIe siècle |
Martin Grandin cite la solution de Pierre Rémond
de Montmort et les deux solutions
obtenues par Abraham de Moivre et par de Mairan. |
|
|
1759 Publié en 1766 |
Euler étudie
le périple du cavalier et propose la solution de divers problèmes comme
comment obtenir un trajet complet à partir de trajets partiels (suggéré par
L.Bertrand). Il propose 54 périples dont 9 sont fermés ou réentrants comme
disait Euler. Sa publication à l'Académie Royale: Solution
d'une question curieuse qui ne paroit soumise a aucune analyse. |
|
|
XIXe siècle |
Rajah Krishnaraja Wadiyar III : un des premiers
parcours du type carré magique |
|
|
1888 |
Tentatives de carré magiques, en fait, semi-magique
(hors diagonales). 83 tels parcours (dont 27 fermés) ont été déposés au
Conservatoire National des Arts et Métiers. |
|
|
2003 – J. C. Meyrignac et Guenter
Stertenbrink |
Recherche exhaustive (62 jours
de calculs): sur un échiquier il existe en tout 140 parcours différents
formant des carrés semi-magiques. Le périple complètement magique est cependant
possible sur des échiquiers 4k × 4k pour k>2. |
|
Voir Historique (très) complet
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()