|
Édition du: 02/04/2024 |
|
INDEX |
Échecs – Cavalier |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
♞ PÉRIPLE du CAVALIER ♞ Carrés magiques et semi-magiques Sur le périple du cavalier
sur un échiquier, on note le numéro du
mouvement pour arriver à chaque case. La grille se trouve ainsi remplie de
nombres de 1 à 64 pour un échiquier classique 8×8. La
question qui se pose: peut-on exécuter un périple
tel que tous ces nombres forment un carré magique ? |
||
|
|
Sommaire de cette page >>> Périples magiques ou semi-magiques |
Débutants Glossaire |
Anglais: The move of a
chess knight, knight's tour / The knight tour problem
|
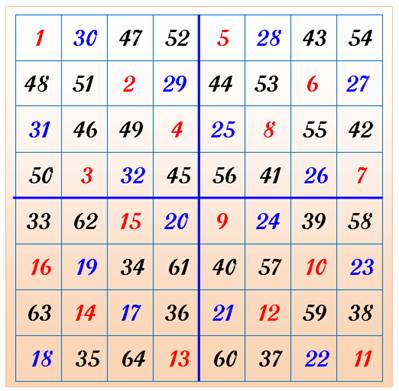
Carré semi-magique La figure ci-contre a été éditée en 1848. La somme sur les lignes et les colonnes donnent
260, mais malheureusement les diagonales ne donnent pas cette somme. Le carré
est semi-magique et non pas magique. Les quatre carrés séparés par les traits bleus
épais sont également semi-magiques
avec 130 pour somme. En coupant encore en carrés de 4 cellules, la somme des
4 nombres est aussi 130 (comme: 1 + 30 + 48 + 51). |
|
||||||||||||
|
Bilan des périples du cavalier en forme de carrés magiques sur une grille de
côté n |
|
||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()