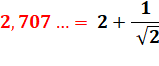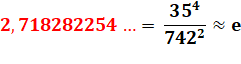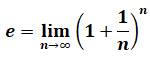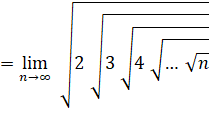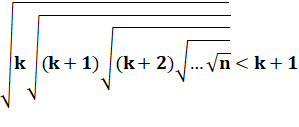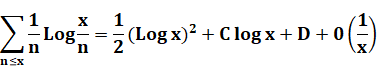nombre – décimales de deux

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/11/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES			Glossaire Nombres
1 0,5 0,1 0,01 0,001 0	2			3 4 / 5 6 / 7 / 8 / 9 10 / 15 20 / 50 100 / 500 1000
Nombre 2	Culture 2	Maths 2	De 2 à 2,7	Expression en 2
Débutant 2	Culture 2 suite	Maths 2 suite	De 2,7 à 3	Proverbes avec 2
Quiz 2	Quantité 2	Binaire	Sciences 2	Dualité

2,7

2,701…

Racine triangulaire de 5.

Taille du carré capable de loger au mieux cinq carrés unités. Démontrée en 1979 par F. Göbel.

2, 714 285 714 = 19 / 7

2, 718 281 828 = e

Écart 0, 003996114, soit: 0, 15 %

Voir Approximations en septièmes.

2, 717 857 143 = 1/1 + 1/2 + … + 1/8

2, 718 281 828 = e

Écart 0, 000424685, soit: 0, 015 %

Écart 4,26 … 10^-7, soir 0,000015 %

Auteur Moody

2,7 1828 1828 4590452354…

Valeur de la constante e.

Valeur de la fonction exp(1) ou

Base des logarithmes naturels (ou népériens)

2, 720 759 220 = (5+10) / 3

2, 718 281 828 = e

Écart 0,002477392, soit: 0,0009 % >>>

2,7474774… = tan (70°)

Curiosité avec cumul de 7.

2,7612068419…

On démontre par récurrence que cette racine à étages est inférieure à 3 en montrant que pour :

On montre que si elle est vraie pour k, elle est vraie pour k – 1.

Cosmologie

2, 7 0,017 K Température du rayonnement fossile.

>>>

Algèbre

D = 2,723... et C = 0, 57… Constantes d'Euler.

Constantes dans la relation suivante:

Géométrie

2,726 833 …= Log 20 / Log 3

Dimension fractale de l'éponge de Menger.

>>>

2,8

		Somme des inverses des nombres de Catalan.
2,807 770 242 028 …	Constante de Fransen-Robinson Valeur de l'aire sous la courbe 1 / Gamma(x) de zéro à l'infini
2, 828 … = 8 = 2 2, 828 4271247 …	Racine de huit. Périmètre du carré de diagonale unité.
2,828 … = 7 129 / 2 520 = 2, 82896 825396 825396 … = 1/1 + 1/2 + 1/3 + … + 1/9	Nombre harmonique: somme des inverses des chiffres de 1 à 9.