|
|||||||||||||||||||||||||||||||||
![]()
|
Algorithme LLL Depuis son invention en 1982 par Lenstra,
Lenstra et Lovasz, l’algorithme
LLL a joué un grand rôle dans plusieurs domaines, en particulier en théorie algorithmique
des nombres et en cryptographie. Notamment:
Prix Abel pour l'année 2021 pour:
|
|
|
|
|
L'algorithme
LLL concerne la manipulation de données dans des graphes
et des réseaux. Le terme
générique réseau définit un ensemble
d'entités (objets, personnes, etc.) interconnectées les unes avec les autres.
Ceux-ci
ne sont pas les réseaux de la vie réelle (réseaux informatiques ou réseaux
sociaux) mais, une abstraction où des entités se définissent par les
relations qu'elles entretiennent entre elles (d'où la notion de graphe ou de
réseaux). Il s'en
suit une série de propriétés complexes et ces algorithmes sont évidemment
largement utilisés par les secteurs de l'informatique et des domaines
connexes. Par
exemple, l'algorithme LLL est surtout utilisé dans un contexte de recherche
de factorisation,
lui-même utilisé abondement dans les algorithmes de cryptographie
où on utilise le caractère difficilement réversible de certaines
factorisation. Cet
algorithme est surtout utilisé pour "casser" les systèmes basés sur
le système RSA, un des plus utilisé des systèmes de
cryptographie. |
|
Pour information: l'algorithme
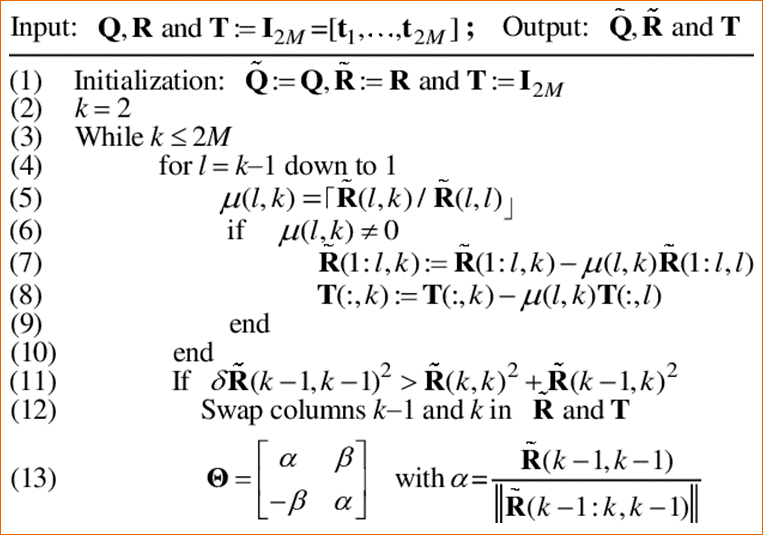
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()
