|
Édition du: 02/12/2024 |
|
INDEX |
CONSTRUCTIONS |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Construction du centre du cercle On nous
propose un cercle dont on ne connait pas l'emplacement de son centre. |
||
|
|
Sommaire de cette page >>> La méthode du livre ou de l'équerre >>> La méthode règle et compas >>> La méthode règle seule ou méthode allumettes >>> La méthode compas seul ou méthode Napoléon >>> La méthode compas seul ou méthode Mascheroni |
Débutants Glossaire |
|
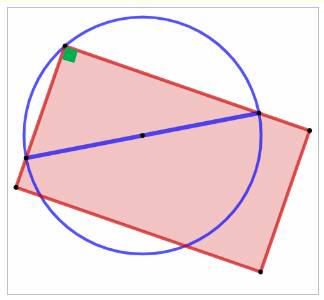
Construction avec un livre ou une
feuille de papier Pour trouver le centre du cercle avec un livre,
mettre un coin du livre sur le cercle (en ce coin, il y a un angle droit). Noter les deux points d'intersection du livre
avec le cercle. Le segment les rejoignant est un
diamètre. Recommencer l'opération avec un autre point du
cercle pour disposer d'un second diamètre. L'intersection des deux diamètres est le centre. Évidemment cette méthode est réalisable avec tout
objet possédant un angle droit, en premier lieu, une équerre. |
|
|
|
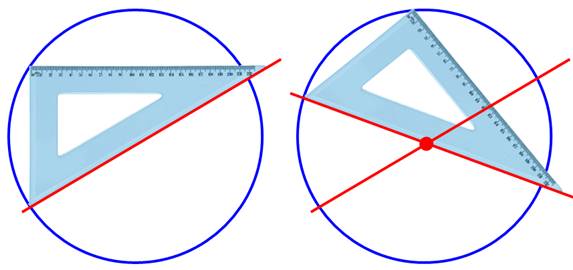
Construction du centre avec une
équerre
|
||
|
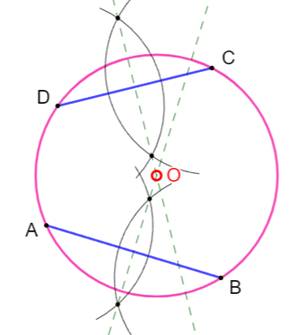
Construction Choisir quatre points sur le cercle: A, B, C et
D. Tracer les deux segments AB et CD (les points a
et d peuvent être confondus). Construire leur médiatrice:
cercles de même rayon issus de chacun des quatre points. Leur point d'intersection est le centre du cercle Justification En effet, la médiatrice d'une corde passe par le
centre du cercle. Dit-autrement, le point central est à égale
distance des extrémités de la corde; distance qui est égale au rayon du
cercle. |
Construction classique du centre
|
|
Voir Constructions
élémentaires
|
But Construire le centre d'un cercle en ne disposant
que d'une règle. En fait, c'est une règle de longueur donnée qui sera
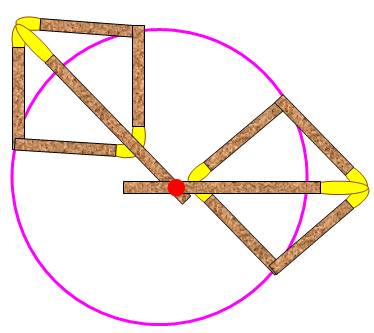
utilisée en tant qu'unité de longueur. C'est les cas des allumettes. Construction La construction ressemble à celle décrite
ci-dessus. Une extrémité des allumettes est placée su le
cercle et l'autre rejoint l'extrémité d'une autre allumette. Deux allumettes plus grandes sont utilisées pour
joindre les extrémités réunies. Elles se coupent au centre du cercle. Plus l'allumette ou la règle est fine, plus la
construction sera précise. |
Construction du centre avec des
allumettes
|
|
|
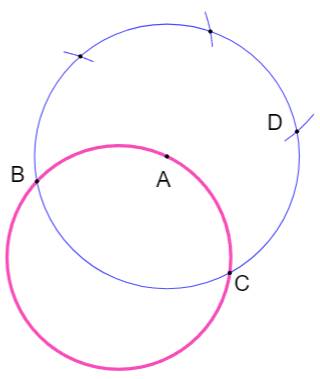
Construction – Figure 1 Un cercle rose et un point A quelconque sur le
cercle. Un cercle bleu de centre A et de rayon
quelconque. Il coupe le cercle initial en B et C. À partir du point B et avec le rayon BA, reporter
le cercle trois fois pour atteindre le point D. Le cercle ayant été découpé en sixième, le
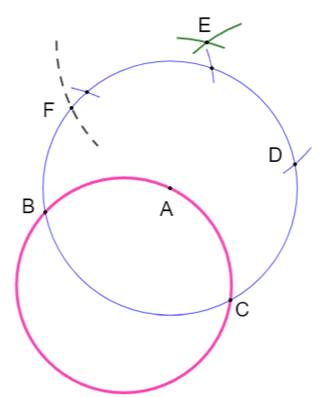
point D est diamétralement opposé à B. Figure 2 Avec le rayon CD, tracer les deux cercles de
centre A et D qui se coupent en E (arcs verts). Avec le même rayon DC et avec E pour centre
tracer le cercle qui détermine le point F (pointillés). On dispose alors
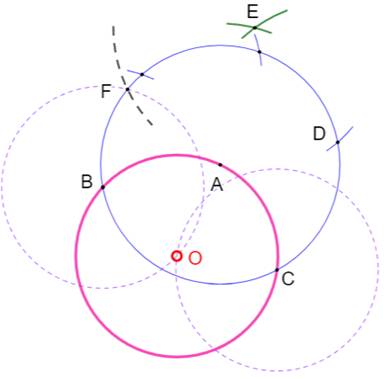
d'une longueur BF qui est précisément le rayon du cercle initial. Figure 3 Deux cercles avec ce rayon BF de centres B et C
(pointillés) se coupent en O, le centre du cercle. |
Figure 1
|
|
|
Figure 2
|
Figure 3
|
|
|
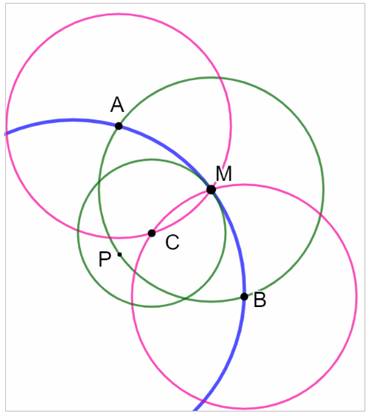
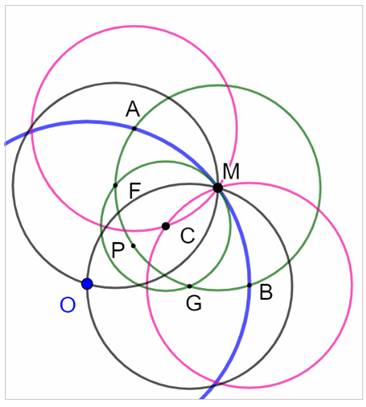
But Construire le centre du cercle avec le compas
uniquement. Le problème, dit de Napoléon, porte le n°145 dans Géométrie du
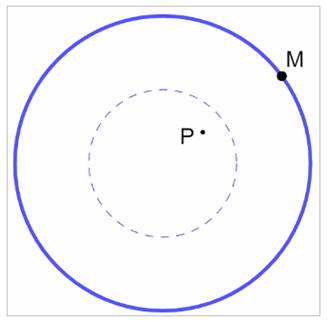
compas de Lorenzo Mascheroni. Construction – Figure 1 – Bleu On choisit un point M sur le
cercle et un point P dans la zone d'un
cercle de rayon moitié de l'original (en gros). Figure 2 – Vert Le cercle de centre M et de rayon PM crée les
intersections A et B ? On trace les cercles de centres A et B et de
rayon AM qui se coupent en C. Nouveau cercle de centre C et de rayon CM. Figure 3 – Roses Il coupe le petit cercle vert en F et G. Les cercles de centres F et G et de rayon FM
(noirs) se coupent en O, le centre du cercle initial. |
Figure 1
|
|
|
|
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |