NOMBRES - Curiosités, théorie et usages

Accueil / Dictionnaire / Rubriques / Index / Atlas /  Références /    Nouveautés

ORIENTATION GÉNÉRALE    -   M'écrire   -   Édition du: 04/07/2009

Débutants

Général

RUBRIQUE   Nombres Homogènes

Glossaire Général

 

JEUX des équations

 

 

Sommaire de cette page

>>> APPROCHE

>>> TRIANGLE
>>> CARRÉ
>>> PENTAGONE

>>> ÉTOILES

>>> HEXAGONES

 

 

 

 

 

Approche

 

*   Il s'agit de trouver la solution d'équations mettant en jeu les nombres homogènes.

*   Vous trouverez un excellent exemple d'énigme avec ces équations dans le roman 676 de Yan Gérard.

*   Prenons les nombres 2, 5 et 12 et formons le tableau suivant:

 

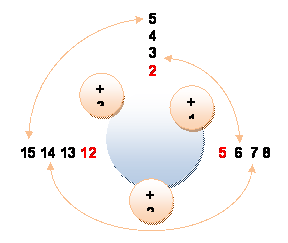
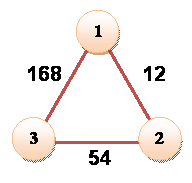
On ajoute 1 aux deux premiers et 2 aux deux suivants, puis 3 aux deux suivants (par permutation circulaire).

 

Chaque couple de deux est formé d'un nombre et d'un de ses multiples.

Dit autrement: les nombres du couple ne sont pas étrangers; leur PGCD est différent de 1.

 

*   L'idée est de faire la même chose avec les nombres homogènes.

 

 

Tableau

 

+1

+2

+3

2

3

 

5

5

6

7

 

12

 

14

15

PGCD

3

7

5

 

Illustration

 

Ce triplet {2, 5, 12}

est le plus petit avec cette propriété

 

 

 

 

TROIS ÉQUATIONS - Triangle

 

*   Le principe est le même, avec une contrainte supplémentaire:

-         Chacun des deux nombres du couple doit être formé des mêmes facteurs à une puissance ou une autre.

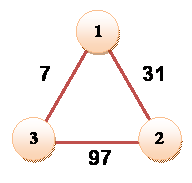
-         Dit autrement, les deux nombres doivent être homogènes.

Dans l'exemple en haut, 7 et 14  (14 = 7 x 2) ne sont pas homogènes et cet exemple ne répond pas à notre exigence.

Dans l'exemple ci-dessous en haut, 50 et 80 sont homogènes car ils possèdent les mêmes facteurs premiers 2 et 5. Le produit 2 x 5 = 10 est le nombre simple, "père" des nombres homogènes de la même famille.

 

 

 

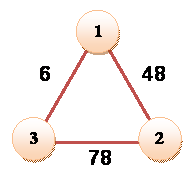
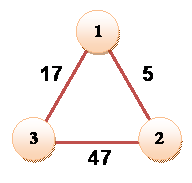
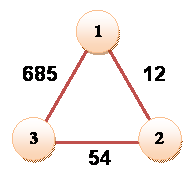
Voici les cinq seules solutions pour des nombres jusqu'à 1000

 

Ces triplets sont cités dans le roman 676 de Yan Gérard

 

 

Tableau avec calcul

 

 

+ 1

+ 2

+ 3

6

7

 

9

48

49

50

 

78

 

80

81

Simple

7

2 x 5

9

Vérification

        7

49 = 7²

50 = 2² x 5²

80 = 24 x 5

       9

81 = 9²

 

 

+ 1

+ 2

+ 3

7

8

 

10

31

32

33

 

97

 

99

100

Simple

2

3 x 11

2 x 5

Vérification

  8 = 23

32 = 25

33 = 3x11

99 = 3²x11

 10 = 2x5

100=2²x5²

 

 

+ 1

+ 2

+ 3

17

18

 

20

5

6

7

 

47

 

49

50

Simple

2 x 3

7

2 x 5

Vérification

18 = 2x3²

  6 = 2x3

       7

49 = 7²

20 = 2²x5

50 = 2x5²

 

 

 

 

Illustration

 

 

 

 

Suite avec CARRÉS et PENTAGONES

 

 

 

Voir

*  Nombres homogènes

Aussi

*  Carrés magiques

*  Sudoku

Sites

*