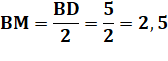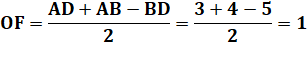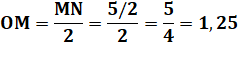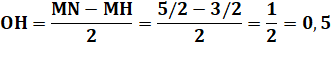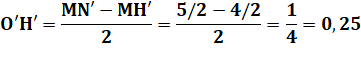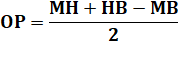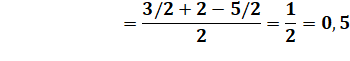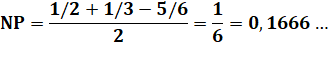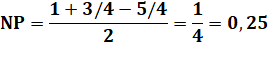Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/02/2025 M'écrire Brèves de Maths

INDEX Types de nombres	Triangle rectangle et ses cercles
	Rectangle	Isiaque ou 345	Propriétés diverses
	Congruents	de Pythagore	Constructions
	T345 et ses cercles

Faites un double-clic pour un retour en haut de page

Triangle rectangle 345 et ses cercles Le fameux triangle rectangle 345 (dit aussi: isiaque) et toutes les possibilités de cercles construits autour de lui.
	Sommaire de cette page >>> Florilège de cercles associés au triangle 345 >>> Cercles inscrit et circonscrit >>> Cercles sur l'hypoténuse >>> Cercles latéraux >>> Cercles internes >>> Cercles latéraux aux internes	Débutants Triangle Glossaire Triangle

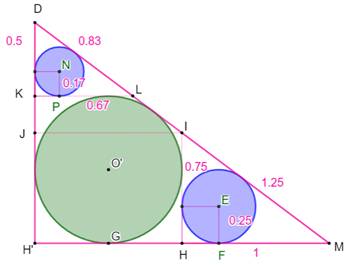
Florilège de cercles associés au triangle 345

Nombres et fractions indiquent le rayon du cercle

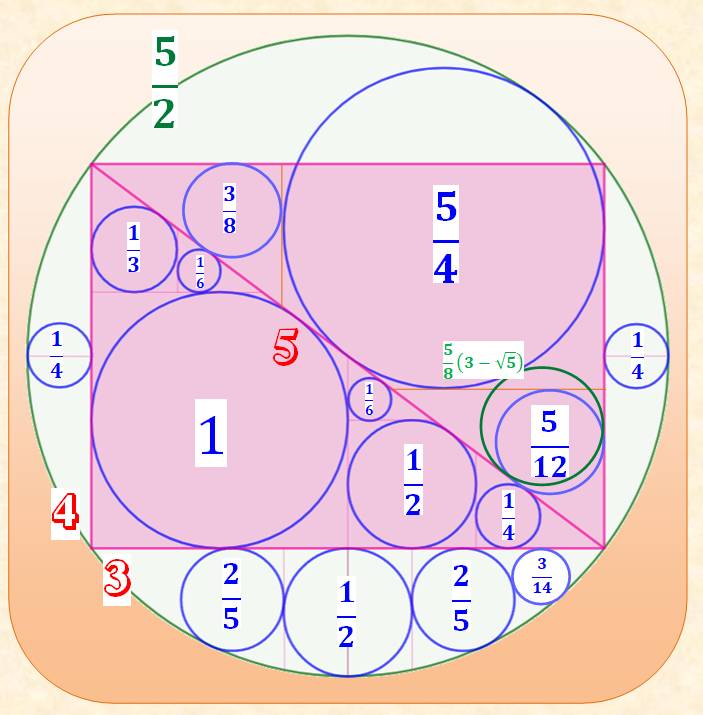
Voir Brève 61-1212

Cercles inscrit et circonscrit		haut
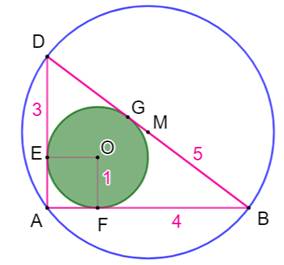
Construction Le triangle rectangle ABD avec pour côtés 3, 4 et 5. Le cercle inscrit au triangle rectangle (vert). Le cercle circonscrit au triangle rectangle (bleu). Calculer le rayon de ces deux cercles. Cercle circonscrit Le triangle rectangle ABD avec son angle droit en A est inscrit dans un demi-cercle dont le diamètre est BD. Rayon du cercle bleu: Cercle inscrit On connait la formule du rayon en fonction des côtés:

Cercles sur l'hypoténuse		haut
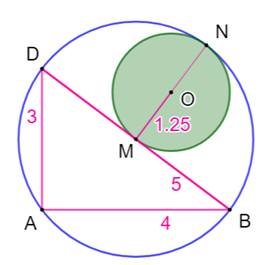
Construction Du point M, milieu de BD, la perpendiculaire à BD. Intersection avec le cercle en N. Cercle vert de centre O, milieu de MN et de rayon OM. Ce cercle est tangent à l'hypoténuse BD et au cercle vert. Rayon du cercle bleu Le segment MN est un rayon du cercle bleu;
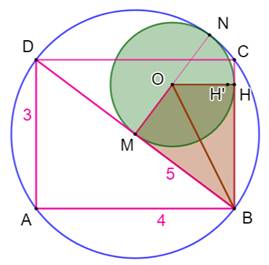
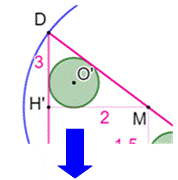
Construction du rectangle et question Le triangle ABD est dupliqué pour formé le rectangle ABCD. On trace la tangente BH' au cercle vert. L'angle OH'B est droit. On trace OH perpendiculaire au côté BC. Toutes les deux issues de B et faisant un angle droit avec elle, les droites OH et OH' sont confondues et avec elles les points H et H' Le cercle vert est aussi tangent au côté BC du rectangle.

Cercles latéraux		haut
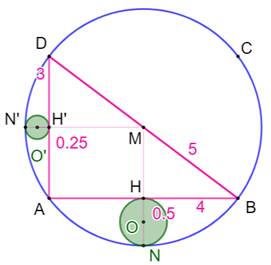
Construction Perpendiculaire en M au côté AB du triangle. Intersection H avec AB et N avec le cercle bleu. Cercle de diamètre HN. Idem pour le côté AD. Rayon du cercle de centre O Le segment MN est un rayon du cercle bleu; Rayon du cercle de centre O' Le segment MN' est un rayon du cercle bleu;

Cercles internes		haut
Construction Cercles inscrits dans les triangles MHB et MH'D. Piste Les triangles HMB et H'MD sont isométriques Les deux cercles inscrits sont bien entendu identiques. Rayon de chacun des deux cercles Formule du cercle inscrit:

Cercles latéraux aux internes		haut
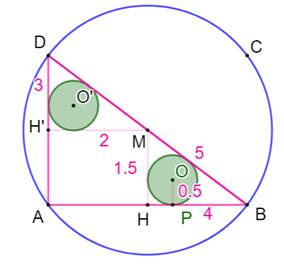
Construction Dans le petit triangle supérieur H'MD, avec son cercle inscrit, on dessine deux nouveaux cercles inscrits dans les triangles rectangles dont un des côtés est une tangente au cercle vert. Piste On calcule simplement les dimensions et on applique la formule du cercle inscrit: Rayon du cercle bleu en haut Rayon du cercle bleu en bas

Les rayons des autres cercles de la figure initiale se calculent sur le même principe …

Haut de page (ou double-clic)

Retour	Triangle rectangle – Index
Suite	Triangle équilatéral Triangle rectangle – Constructions Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/T345Cerc.htm