addition avec les plus et les moins débutant exemples

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/09/2018 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	INITIATION au CALCUL
Débutants Nombres	SOUSTRACTION		Glossaire Nombres
INDEX CALCULS	Soustraction simple	Initiation
	Nombres négatifs	Ascenseur
	Additions et soustractions des nombres négatifs	Traits verts et traits rouges
		Exemples
		Poids et ballons
	Sommaire de cette page >>> Addition à partir de 0 >>> Soustraction à partir de 0 >>> Addition à partir d'un nombre PLUS >>> Soustraction à partir d'un nombre PLUS >>> BILAN

Les PLUS et les MOINS

Explications pas à pas

Exemples d'application de la recette des additions et des soustractions avec des plus et des moins.

Le moins est plus fort que le plus.

Sauf s'ils sont deux, alors ils retournent en plus.

Pour ceux qui veulent comprendre en douceur.

0 + 3 = ?

Je sais que si je n'ai pas de bonbons et que l'on m'en donne 3, j'aurai 3 bonbons au total. Facile!

Illustration
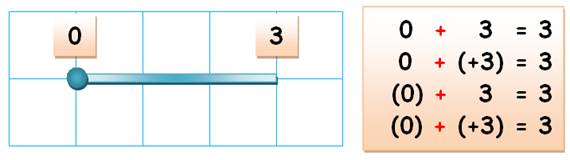
Je montre +3 sur le dessin (Comme si je montais au 3^e étage).

Ça fait toujours 3, même si les nombres sont emballés dans des parenthèses.

Avec les PLUS, les parenthèses ne servent rien.

On sait que, "Rien + 3 Bonbons" c'est la même chose que "3 Bonbons + Rien". À la fin, j'ai toujours "3 bonbons".

0 + 3 = 3 + 0 = 3

Je peux changer l'ordre des termes dans l'addition.

0 - 3 = ?

Comment est-il possible que l'on me demande 3 bonbons alors que je n'en ai pas ? C'est sans doute que, tu en dois 3 à ton copain. Tu as mangé les 3 bonbons qu'il ta prêté. On dit que tu as une dette de 3. Autrement-dit tu en as –3.

Illustration
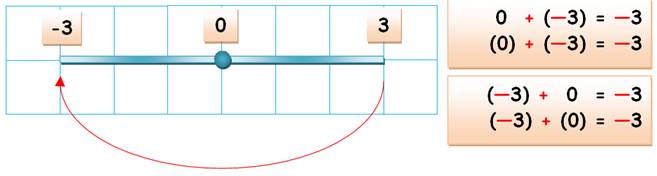
Je montre –3 sur le dessin (Comme si je descendais au 3^e sous-sol).

Avec un signe MOINS, je bascule le 3 de l'autre côté.

Les parenthèses servent à emballer le nombre avec son signe moins, pour bien indiquer qu'il s'agit de –3. Ce –3 forme un tout, un bloc.

Nous avons vu que l'on peut changer l'ordre des termes sans changer le résultat: 0 + (–3) = (–3) + 0 = –3 .
Pourvu que les moins restent bien "emballés" lorsqu'on fait cet échange.

2 + 3 = ?

Si j'ai déjà 2 bonbons et que l'on m'en donne 3, j'aurai 5 bonbons au total. Encore très facile!

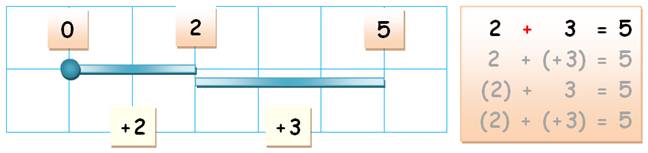
Illustration Je montre 2 + 3 sur le dessin
(Je suis au 2^e étage et je monte 3 étages de plus).

L'addition consiste à mettre les deux traits bout à bout vers la droite: l'un qui mesure 2 et l'autre qui mesure 3. L'ensemble mesure 5.

On se souvient que les parenthèses sont inutiles.

2 – 3 = ?

Si j'ai déjà 2 bonbons et j'en donne trois 3 à Louise, c'est impossible.

Sauf si je demande à Clément de m'en prêter 1. Alors je pourrai en donner 3 à Louise, mais j'en devrai 1 à Clément. On peut dire que j'en ai -1.

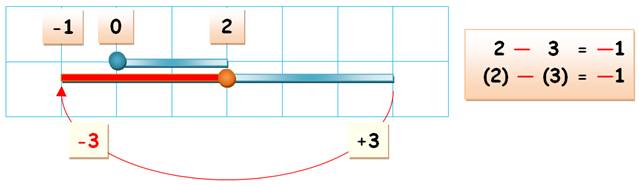
Illustration Je montre 2 – 3 sur le dessin. (Je suis au 2^e étage et descends de 3 étages. J'arrive au premier sous-sol).

La soustraction consiste à ajouter le second trait mais dans l'autre sens, vers la gauche. Si bien que le bout de l'ensemble tombe sur le -1.

Pour soustraire 3, je le bascule de l'autre côté.

Si j'ai 5 bonbons et que j'en mange 1, ce n'est pas la même chose que si j'en ai 1 et que j'en mange 5.

5 – 1 = 4 est différent de 1 – 5 = – 4

Avec des MOINS, je ne peux pas changer l'ordre des termes.

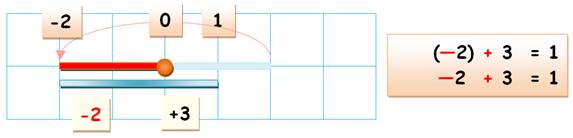
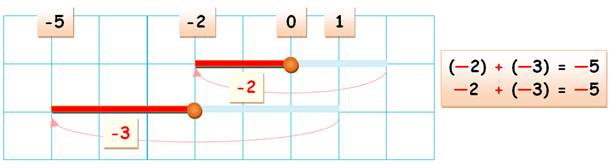
–2 + 3 = ? et –2 + (–3) = ?

Si je dois 2 bonbons et que l'on m'en donne 3, je rembourse les 2 et il m'en reste 1.

Illustration Je montre –2 + 3 sur le dessin
(Je suis au 2^e sous-sol et je monte 3 niveaux).

Je commence par placer mon trait de 2 en le basculant pour faire –2 et j'ajoute un trait de 3, donc vers la droite). Le bout tombe sur 1.

Illustration Je montre –2 et –3 à la suite 3 sur le dessin
(Je suis au 2^e sous-sol et descends encore de 3 niveaux).

Je bascule dans l'autre sens tous les nombres avec MOINS.

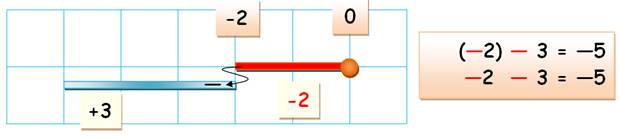
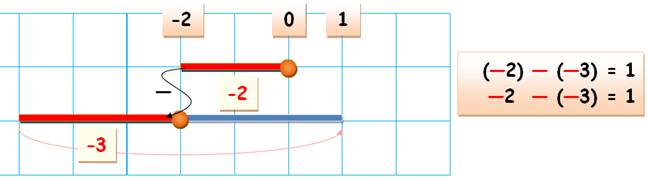
–2 – 3 = ? et –2 – (–3) = ?

Illustration Je montre –2 et –3 à la suite sur le dessin
(Je suis au 2^e sous-sol et descends encore de 3 niveaux).

Pour faire une soustraction, je place le trait au bout du précédent (au bout du -2), mais vers la gauche.

Illustration Je montre –2 et –3 à la suite sur le dessin
(Je suis au 2^e sous-sol et je fais le contraire de descendre 3 niveaux).

Pour faire une soustraction, je place le trait au bout du précédent (au bout du –2). Il s'agit d'un nombre négatif (–3), alors il bascule dans l'autre sens. Le total est l'équivalent de –2 + 3 = 1.

BILAN – C'est toujours sans problème sauf les cas en rouge où –(–3) = +3
	Addition	Soustraction
De 0 Avec nombre positif	0 + 2 = 2	0 – 3 = - 3
De 0 Avec nombre négatif	0 + (-2) = -2 0 – 2 = -2	0 – (-3) = 3 0 + 3) = 3
D'un nombre positif Avec nombre positif	5 + 2 = 7	5 – 3 = 2
D'un nombre positif Avec nombre négatif	5 + (-2) = 3 5 – 2 = 3	5 – (-3) = 8 5 + 3 = 8
D'un nombre négatif Avec nombre positif	-5 + 2 = -3	-5 – 3 = -8
D'un nombre négatif Avec nombre négatif	-5 + (-2) = -7 -5 – 2 = -7	-5 – (-3) = -2 -5 + 3 = -2
Le MOINS l'emporte sur le PLUS. Le MOINS et le MOINS se retournent en PLUS.

Exemple 1

3 + 2 – 4 + (– 2) – (– 3)

Exemple simple expliqué en détail en >>>

3 + 2 – 4 + (– 2) – (– 3)

3 + 2 – 4 – 2 + 3

5 – 4 – 2 + 3

1 – 2 + 3

– 1 + 3

Exemple 2

(3+2) + (5–7) + 2 + (–3) – (4–5) – ((–3) – (–5))

Nous calculons en priorité dans les parenthèses

(3+2) + (5–7) + 2 + (–3) – (4–5) – ((–3) – (–5))

( 5) + ((-2)) + 2 + (–3) – (-1) – ((–3) + 5)

Nous progressons pas à pas

5 – 2 + 2 – 3 +1 – (2)

3 + 2 – 3 +1 – 2

5 – 3 + 1 – 2

2 + 1 – 2

3 – 2

Exemple 3

(((3+2) – (5–7)) – 2 – ((–3) – (4–5))) – ((–3) – (–5))

Nous calculons en priorité dans les parenthèses les plus profondes

(((3+2) – (5–7)) – 2 – ((–3) – (4–5))) – ((–3) – (–5))

(((5) – (–2)) – 2 – ((–3) – (–1))) – (+2)

(((5) – (–2)) – 2 – ((–3) – (–1 ))) – (+2)

((7) – 2 – (–2)) – (+2)

(7 – 2 +2) – (+2)

7 – (+2)

7 – 2

Retour

Additions et soustractions avec des plus et des moins

Encore des exemples

Initiation aux calculs

Suite

Addition – Débutant

Addition en plus et en moins: même sujet que cette page, sous l'angle des équations (poids et ballons)

Voir

Débutants – Index

Algèbre – Débutant