NOMBRES - Curiosités, théorie et usages

Accueil / Dictionnaire / Rubriques / Index / Atlas / Références /    Nouveautés

ORIENTATION GÉNÉRALE    -   M'écrire   -   Édition du: 02/04/2010

Débutants

Nombres

Premiers

Nombres PREMIERS

Glossaire

Nombres

Premiers

 

Historique

 

 

 

Index des pages

NOMBRES PREMIERS

 

>>> INDEX

 

Historique

Historique - Ordi

Historique de Pi (n)

 

Sommaire de cette page

>>> Avec les ordinateurs

>>> Records - le plus grand connu

>>> Petite histoire moderne

 

 

 

NOMBRES PREMIERS – Historique
 

*    Utilisation des ordinateurs, et la course aux records se poursuit de plus belle.

 

 

RECHERCHES AVEC LES ORDINATEURS 

 

Miller et Wheeler (en 1951)

*         Ils trouvent plusieurs premiers avec les ordinateurs:  k.M127 + 1 pour k = 114, 124, 388, 408, 498, 696, 738, 744, 780, 934 et 978.

 

*         De même que le nouveau record à 79 chiffres: 180(M127)2 + 1 avec M127 = 2127 – 1.

 

 

 

Raphael Robinson

*         Le record ne résista pas longtemps.

*         L'année suivante, Raphael Robinson découvre 5 nouveaux Mersenne avec l'ordinateur SWAC (Standards Western Automatic Computer). Le programme marcha du premier coup et donna 2 nouveaux premiers le jour même. Il écrivit: "Le programme fut essayé le 30 janvier et le jour même

M521 et

M607 furent trouvés.

 

*         Trois autres suivirent :

M1279 le 25 juin,

M2203 le 7 octobre et

M2281 le 9 octobre."

 

 

A noter que, en 1949, Newman utilisa le prototype de l'ordinateur Manchester pour faire les premiers essais de recherche automatique.

 

 

Alan Turing

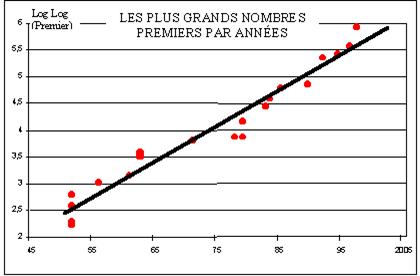
*         Turing améliore ce programme. On lui prête parfois la paternité de la recherche des premiers par ordinateurs.

 

 

 

 

Premier bilan des recherches par ordinateurs

 

 

*         Les records de Miller, Wheeler, et Robinson sont les premiers points du graphique.

*         En ordonnées, Log Log donne le nombre de chiffres de l'exposant de la puissance de 10: 10123 => Log Log = 3.

 

 

Les progrès suivent la performance croissante des ordinateurs

*         Riesel trouve M3217 avec la machine suédoise BESK.
 

*         Hurwitz trouve M4253 and M4423 avec l'IBM 7090.
 

*         Gillies utilise l'ILLIAC-2 et trouve M9689, M9941 and M11213

*         Tuckerman trouve M19937 avec un IBM 360.

 

*         Du fait de l'organisation des calculs, Hurwitz trouve M4423 quelques secondes avant M4253

*         Tous les Mersenne du tableau ci-dessous ont été trouvés avec le test de Lucas - Lehmer. Les deux autres en utilisant le théorème de Proth. 

 

   

 

BILAN des records "ordinateurs" 

Nombre

Chiffre

Année

Machine

Par qui

180 (M127)2 + 1

79

1951

EDSAC 1

Miller & Wheeler

M521

157

1952

SWAC

Robinson (30 Jan)

M607

183

1952

SWAC

Robinson (30 Jan)

M1279

386

1952

SWAC

Robinson (25 Juin)

M2203

664

1952

SWAC

Robinson (7 Octobre)

M2281

687

1952

SWAC

Robinson (9 Octobre)

M3217

969

1957

BESK

Riesel

M4423

1332

1961

IBM 7090

Hurwitz

M9689

2917

1963

ILLIAC 2

Gillies

M9941

2993

1963

ILLIAC 2

Gillies

M11213

3376

1963

ILLIAC 2

Gillies

M19937

6002

1971

IBM 360/91

Tukerman

M21701

6533

1978

Cyber 174

Noll & Nickel

M23209

6987

1979

Cyber 174

Noll

M44497

13395

1979

Cray 1

Nelson & Slowinski

M86243

25962

1982

Cray 1

Slowinski

M132049

39751

1983

Cray X - MP

Slowinski

M216091

65050

1985

Cray X - MP

Slowinski

391581 x 2216193 – 1

65087

1989

Amdahl 1200

Amdahl Six : Brown, Noll,

Parady, Smith, Zarantonello

M756839

227832

1992

Cray -2

Slowinski & Gage

M859433

258716

1994

Cray C90

Slowinski & Gage

M1257787

378632

1996

Cray T94

Slowinski & Gage

M1398269

420921

1996

Pentium ( 90 MHz)

Armengaud, Woltman, GIMPS

M2976221

895932

1997

Pentium (100 MHz)

Spence, Woltman, GIMPS

M3021377

909526

1998

Pentium (200 MHz)

Clarkson, Woltman, Kurowski, GIMPS

M6 972 593

2 098 960

1999

 

Hajratwala, Woltman, Kurowski
& GIMPS, PrimeNet

SUITE

*    Les plus grands premiers connus >>>

*    Liste de tous les nombres de Mersenne premiers connus >>>

 

 

  

Petite histoire moderne

 

Après avoir trouvé le 23e premier de Mersenne

*         à l'Université de l'Illinois, le département des mathématiques fut si fier qu'elle fit imprimer sur ses enveloppes :

" 211213-1 est premier ".

 

Les 25e et 26e nombres premiers de Mersenne

*         Ils furent trouvés par des étudiants Laura Nickel and Curt Noll, bien que ne connaissant que peu les mathématiques utilisées pour le test de Lucas.

*         Utilisation du supercalculateur de l'université (CSUH's CDC 174).

*         Leur découverte fit la une des télévisions et du New York Times.

*         Ensuite, ils travaillèrent chacun de leur côté, mais Noll laissa le programme tourner et après la découverte du 2e (le 26e) revendiqua la découverte complète.

*         Noll continua ses recherches en vain sur Mersenne, mais il détient, en équipe, le record du nombre premier non Mersenne.

*         Il travaille actuellement pour Silicon Graphics.

 

Slowinski

*         Il travaille pour Cray computers, et a écrit une version du test de Lucas adoptée par beaucoup de laboratoires autour du monde.

*         Il le fait fonctionner durant les temps morts de leurs ordinateurs.

*         La recherche de Slowinski n'est pas organisée si systématiquement qu'on le croit (ses propres paroles).

*         Il a trouvé les 30e et 31e, mais a loupé le 29e, trouvé par Colquitt & Welsh.

 

George Woltman

*         Un excellent programmeur et organisateur.

*         À partir de 1995, il forme une base de données unique à partir des bases disparates existantes.

*         Il rend cette base publique et met à disposition un programme très optimisée pour la recherche des Mersenne sur le web (Internet).

 

C'est le début du GIMPS

*         GIMPS: The Great Internet Mersenne Prime Search

*         Programme de recherché coopératif qui a déjà trouvé les trois plus grand Mersenne connus (via Clarkson, Armengaud and Spence).

*         Il explore toutes les régions laissées en friche, combine les efforts de douzaines d'experts et de milliers d'amateurs.

 

 

Scott Kurowski (En 1997) et bien d'autres

*         Ils mettent en place le PrimeNet pour automatiser la sélection des zones de recherche et la synthèse des résultats.

*         Maintenant presque tout le monde peut se joindre à la recherche.

 

 

 

 

 

Retour

*    Historique des nombres premiers avant les ordinateurs

Suite

*    Historique sur la quantité des nombres premiers

*    Nombres premiers – Index

Voir

*    Histoire – Index

*    Table des records

*    Tous les Mersenne premiers