NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	EXPOSANTS
Débutants Général	RACINES 13^e				Glossaire Général
INDEX Racine Calcul mental	Règles de base =>	Principe	Unités et dizaines	Poids forts
	2 chiffres =>	Dizaine impaire	Dizaine paire
		Sommaire de cette page >>> Nombres en …1 >>> Nombres en …7 >>> Nombres en …3 >>> Nombres en …9

RACINE TREIZIÈME

Racine à deux chiffres

Dizaine impaire

Exercice de calcul de racine treizième à portée de tous sur des racines finales ne comportant que deux chiffres. Les puissances peuvent aller jusqu'à 26 chiffres tout de même.

Le chiffre des unités est connu, c'est celui de la puissance. Le second chiffre (dizaine) se déduit de celui des dizaines de la puissance. Cette déduction est relativement aisée pour les unités impaires, sauf pour 5.

Nombres en …1
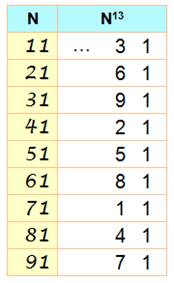
Règle n°2-1 La dizaine de N^13 est égale à 3 fois la dizaine de N (dont on ne conserve que l'unité). Exemple 64610 8188922667 3298932241 Sa racine 13^e : Unité: 1 Dizaine: 4 => 24 = 3 x 8 => 8 Soit: 81^13 Alternative: unité du produit par 7. Exemple: 6 => 7 x 6 = 42 => 2.

Nombres en …7
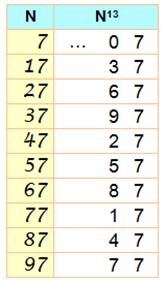
Règle n°2-7 Idem nombre en …1 Exemple 670 4603875249 6061076057 Sa racine 13^e : Unité: 7 Dizaine: 5 => 15 = 3 x 5 => 5 Soit: 57^13 (coquetterie: mêmes dizaines et unités, 57).

Nombres en …3
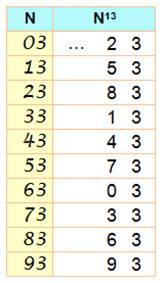
Observations Progression de 3. Avec 0 dans N, je passe à 2 dans N^13 Avec 1 dans N, je passe à 5 dans N^13, soit 1 x 3 + 2 Avec 2 dans N, je passe à 8 dans N^13, soit 2 x 3 + 2 Etc. Règle n°2-3 La dizaine de N^13 est égale à 3 fois la dizaine de N, plus 2 (dont on ne conserve que l'unité). Exemple 16718 4950739378 8885941033 Sa racine 13^e : Unité: 3 Dizaine: 3 => 3 – 2 = 1 => 21 => 3 x 7 Soit: 73^13 Alternative: unité du produit par 7 de la dizaine moins deux. Exemple: 8 => 8 – 2 = 6 => 7 x 6 = 42 => 2.

Nombres en …9
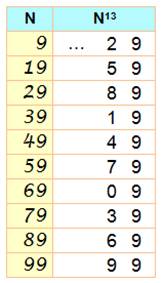
Règle n°2-9 Idem nombre en …3 Exemple 877521 0229989679 8785221299 Sa racine 13^e : Unité: 9 Dizaine: 9 => 9 – 2 = 7 => 27 => 3 x 9 Soit: 99^13 (coquetterie: mêmes dizaines et unités, 99, idem pour 49).

Bilan

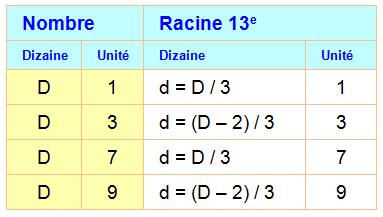
La racine 13^e des nombres avec unité 1, 3, 7 ou 9 et ayant deux chiffres est connue de la manière suivante:

Unité = celle du nombre; et

Dizaine = d calculé comme indiqué sur le tableau. On prend soin d'extrapoler D en multiple de 3. Par exemple D = 2 devient 12, 7 devient 27, etc.

Alternative: Pour 1 et 7 => unité de dizaine fois 7.

Pour 3 et 9 => unité de (dizaine - 2) fois 7.

Suite	Deux chiffres – Dizaine paire
Voir	Racine cubique Racine cinquième
Site	Voir Liste
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Racine13.htm