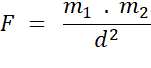|
||||||||||||
![]()
|
Attraction
de la TERRE La Terre, comme tout objet ayant une masse, exerce une force d'attraction sur les autres objets. C'est le cas des objets
de la surface de la Terre qui se trouvent plaqués au sol, comme
irrésistiblement attirés par cette énorme boule de matière qu'est la Terre. C'est le cas d'un astre
proche comme la Lune qui, à tout moment,
est attirée par la Terre, comme tenue par celle-ci par une grande corde. On dit que
la Terre possède un champ
gravitationnel. Champ, car cette force
d'attraction s'exerce en tout point autour de la Terre et à toute altitude. Gravitation, du verbe
graviter qui veut dire tourner autour, évoluer dans le voisinage. |
Vocabulaire:
du particulier terrestre au général dans l'Univers
|
Attraction terrestre Attraction gravitationnelle |
Champ terrestre Champ gravitationnel |
|
Gravitation terrestre ou
Pesanteur Gravitation universelle |
Force d'attraction terrestre Force d'attraction
gravitationnelle |
|
|
||
|
Le poids d'un objet dépend de sa masse et de la
force avec laquelle il est attiré vers le centre de la Terre. Cette force varie en raison inverse du carré de la
distance. Au loin, la force devient si faible, qu'elle est
sans effet.
|
La loi de la gravitation -
Isaac
Newton en 1684. -
Forme
littérale: L'attraction gravitationnelle entre deux
corps est
-
Forme
algébrique:
-
Note: Lorsque l'objet est une sphère homogène
(dont la masse est répartie uniformément), la distance est mesurée à partir
du centre de la sphère. |
|
|
Attraction terrestre avec
l'altitude |
|
|
|
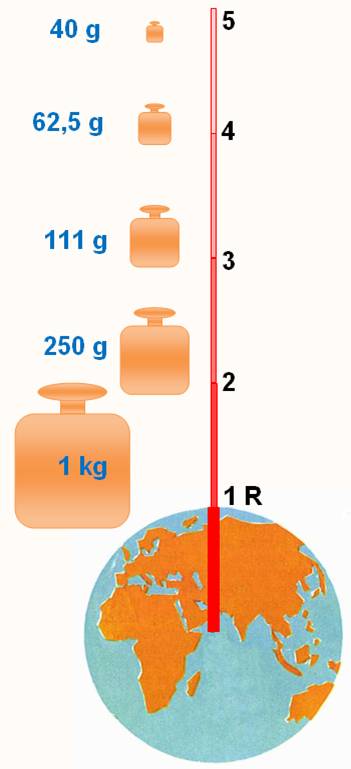
Un objet A qui pèse 1 kilogramme à la surface de la terre pèse de
moins en moins avec l'altitude. À la surface de la Terre, l'objet A est à R = 6
378 km du centre de la Terre. Doublons cette distance en montant à 6 378 km et
le poids sera réduit par 4, soit 250 grammes. Mais il faut monter à 6000 km pour cette
réduction. Quid pour 6000 m seulement? Voyons pour l'Himalaya. |
|
|
|
Au sommet de l'Himalaya à 8700 m, cet objet perdra
un peu moins de 3 grammes en poids. Soit 3 pour mille. Il faut monter à 3 191 m pour perdre 1 pour mille. |
Calcul: MTerre . MObjet = constante
= P . d² 1000 x 6378² = PHimalaya x (6378 +
8,7)² PHimalaya = 997,277 g Perte de poids: 2,72 g |
|
![]()
|
Voir |
|
|
Cette page |
![]()