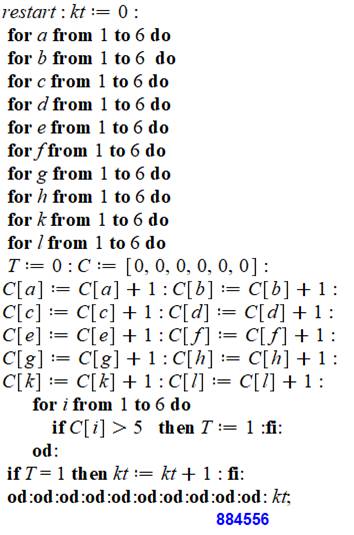Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 17/04/2024 M'écrire Brèves de Maths

INDEX Statistiques Grands nombres Dénombrement	Probabilités avec les dés
	Jeu de dés	Deux dés	Double Six
	Dénombrement	Trois dés	Probabilités et Dés
	Table 1 à 6 dés	Trois dés et une urne
	K chiffres identiques	Proba. mêmes chiffres

Faites un double-clic pour un retour en haut de page

Probabilités de k faces identiques pour n dés lancés Les dés utilisés sont les dés classiques à six faces. Quelle est la probabilité d'avoir, par exemple, 3 chiffres identiques pour un dé lancé six fois (ou un jet de six dés) ? On peut chercher 3 chiffres identiques exactement ou 3 chiffres identiques ou plus. La probabilité peut être calculée par dénombrement des cas favorables ou par des essais statistiques. Attention (notamment pour les programmeurs), les doublons comme 2244 ou 333666 ne seront comptés que pour une seule occurrence.
	Sommaire de cette page >>> Quantité de configurations avec k faces identiques >>> 2 dés – 2 faces identiques >>> 3 dés – 2 faces identiques >>> 4 dés – 2 faces identiques – Calculs >>> 6 dés – 3 faces identiques – Calculs >>> 8 dés – 6 faces identiques – Calculs >>> 10 dés – 6 faces identiques – Calculs >>> Programmation Maple >>> Bilan	Débutants Statistiques Glossaire Probabilités

Quantité de configurations avec k faces identiques au moins

pour un lancé de n dés

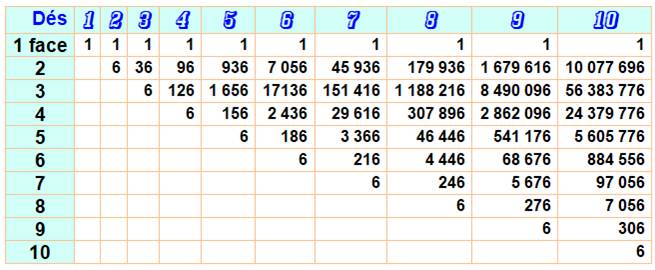
Ex: avec quatre dés, il y a 126 cas où se présentent trois faces identique ou quatre.

C'est à dire le même chiffre, quel que soit ce chiffre de 1 à 6.

2 dés – 2 faces identiques		haut
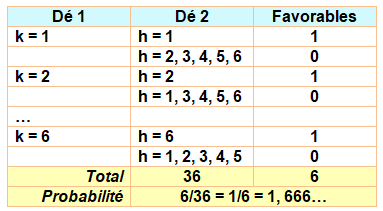
Probabilité d'avoir deux chiffres identiques en lançant deux dés. Les cas possibles sont évidemment:11, 22, 33, 44, 55 ou 66. Voyons une disposition qui servira pour la suite. Si le premier dé donne 1, il y a une seule possibilité pour le second dé: il faut qu'il tombe sur 1 aussi. Même chose pour une autre valeur du premier dé. Soit six cas au total. Ce sont les cas favorables. La totalité des cas est égale à 6 x 6 = 36. La probabilité est le rapport des deux: 6/36 = 1/6.

3 dés – 2 faces identiques		haut
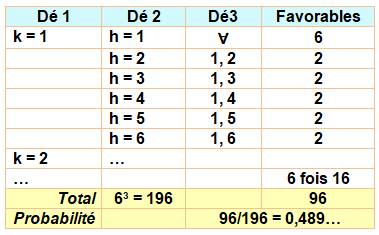
Probabilité d'avoir deux chiffres identiques en lançant le 3 dès. Si le premier est 1, avec 1 pour le deuxième, il y a six possibilités pour le troisième. Avec un autre nombre pour le deuxième, il y a seulement deux possibilités pour le troisième Avec 1 pour le premier, il a 6 + 5 x2 = 16 cas où deux faces sont identiques. On aura donc six cas similaires selon la valeur du premier lancé. Total 6 x 16 = 96 cas où deux faces au moins sont identiques pour un lancé de trois dès.

4 dés – 2 faces identiques – Calculs		haut
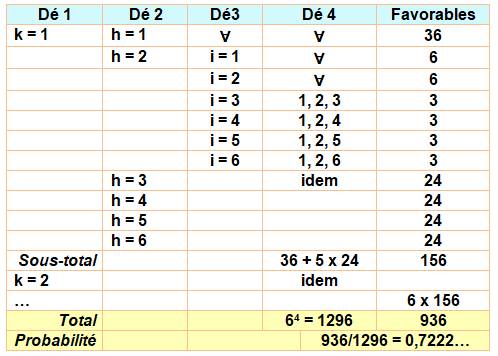
Dénombrement Probabilité d'avoir deux chiffres identiques en lançant le 4 dès. Procédons au décompte comme ci-dessus.

Passons à la théorie: calcul combinatoire

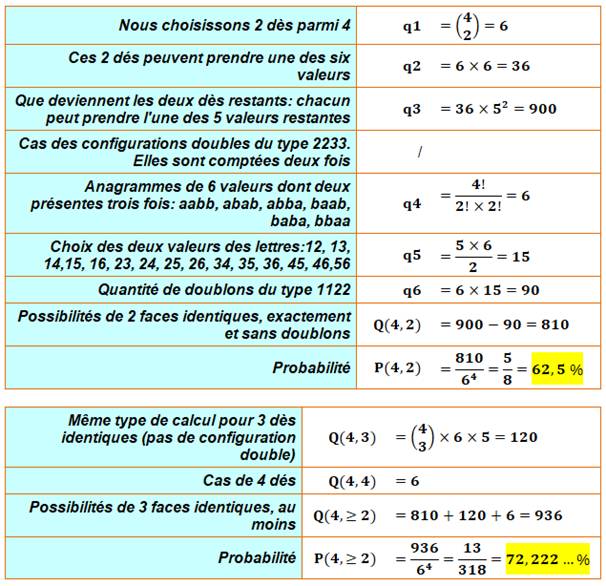
CALCUL FORMEL Exactement Probabilité d'avoir exactement deux chiffres identiques en lançant quatre dès. Rappel Quantité de combinaisons de deux objets parmi quatre. Au moins Probabilité d'avoir au moins deux chiffres identiques en lançant quatre dès.

6 dés – 3 faces identiques – Calculs		haut
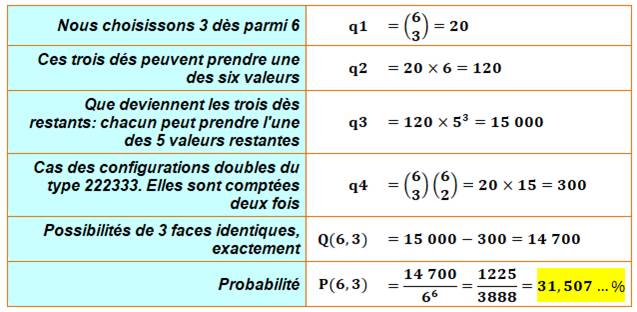
Calcul formel Exactement Probabilité d'avoir exactement trois chiffres identiques en lançant six dès.
Au moins Probabilité d'avoir au moins trois chiffres identiques en lançant six dès.
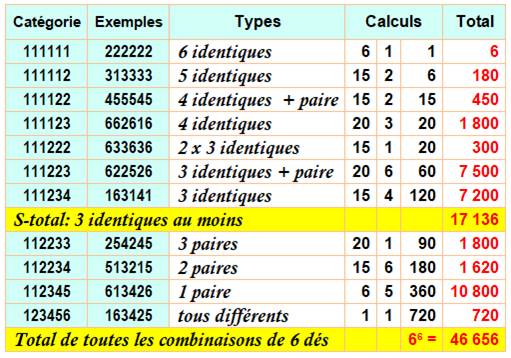
Décompte pour information

8 dés – 6 faces identiques – Calculs		haut
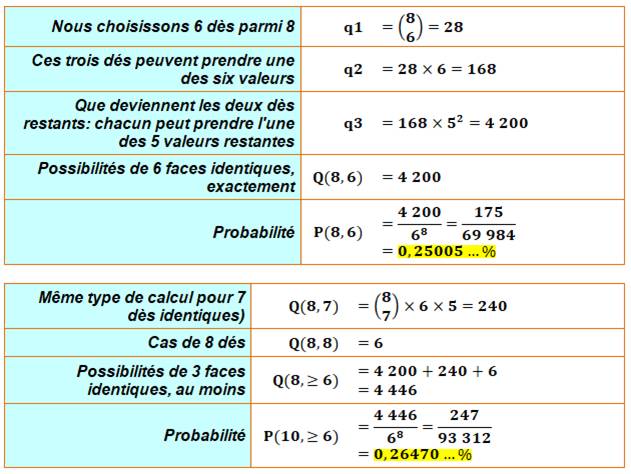
Calcul formel Exactement Probabilité d'avoir exactement six chiffres identiques en lançant huit dès. Au moins Probabilité d'avoir au moins six chiffres identiques en lançant huit dès.

10 dés – 6 faces identiques – Calculs		haut
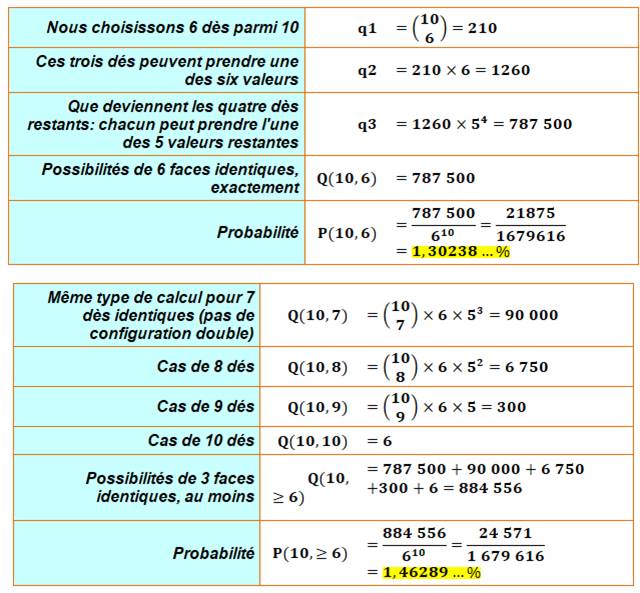
Calcul formel Exactement Probabilité d'avoir exactement six chiffres identiques en lançant dix dès. Au moins Probabilité d'avoir au moins six chiffres identiques en lançant dix dès.
Vérification	La méthode Monte Carlo (jets de dés aléatoires) pour des échantillons de 10^9 lancés donne la valeur 1,46…

Programmation Maple		haut
	Méthode Monte-Carlo But Estimer la probabilité d'au moins six faces identiques pour un lancé de 10 dés. Commentaires Utilisation du lancé de 10 dés au hasard, noté a, b, c… Un vecteur C indique la quantité de fois qu'un chiffre (de 1 à 6) est rencontré lors d'un lancé. Le but consiste à savoir si un des chiffres a été rencontré six fois ou plus. On imprime la quantité de lancés (ktx), la quantité de cas favorables (kt) et la probabilité en pourcentage.
	Méthode du dénombrement But Calculer la quantité de cas où il y a au moins six faces identiques pour un lancé de 10 dés. Commentaires Dix boucles pour positionner chacun des dés. Un vecteur C indique la quantité de fois qu'un chiffre (de 1 à 6) est rencontré lors d'un lancé. Le but consiste à savoir si un des chiffres a été rencontré six fois ou plus. On imprime la quantité de cas favorables qui est celle trouvée par calcul ci-dessus et qui donne ue probabilité de 1,46289 … %

Voir Programmation – Index

Bilan

Les probabilités énoncées ont été vérifiées selon trois méthodes:

Dénombrement à la main pour les petites valeurs et par programme pour les autres;

Calcul formel de combinatoire; et

Méthode Monte-Carlo sur de large échantillons

Haut de page (ou double-clic)

Retour	Voir Haut de page
Suite	36 et dés 421 Courbe en cloche (loi normale) Dénombrement avec des dés Hasard Jeux de dés Paire de dés Probabilités Junior Diaporama Probabilité de sortie du prisonnier Probabilité d'obtenir les mêmes chiffres Six dés Statistiques et probabilités – Index
Voir	Dénombrement et ses applications Échecs Jeux – Index Jeux de hasard (loto, tiercé …) Pentominos Prisonnier et sa probabilité de liberté Trois pièces
Sites	Dice Probability Calculator – Omni calculator Six dices are rolled, what is the probability of getting atleast three same number or face? – Quora – Christopher Pellerito
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Probabil/Deskface.htm