|
||||||||||||
![]()
|
PARTITIONS par des nombres premiers distincts Table donnant la partition
des nombres avec des nombres premiers. Ou avec les carrés des
nombres premiers |
Voir Table des sommes de
premiers consécutifs
|
|
||
|
Table
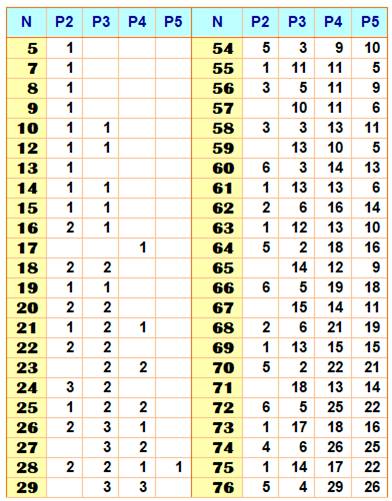
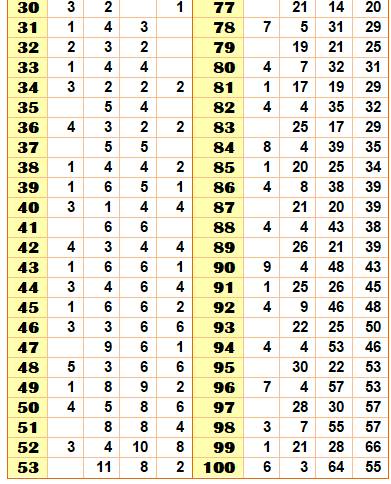
indiquant la quantité de partitions avec de nombres premiers tous différents P2 indique
la quantité de partitions à deux termes; P3 à trois termes; etc. Le nombre 5 est
le plus petit nombre ayant une partition avec deux premiers différents: 5 = 2
+ 3. Le nombre 10 est le
plus petit ayant une partition à deux termes et une partition à trois termes:
10 = 3 + 7 = 2 + 3 + 5 Le nombre 21 est le plus petit ayant, au moins,
une partition à deux termes, une
partition à trois termes et une partition à quatre termes:
= 3 + 5 + 13 = 3 + 7 + 11
= 2 + 3 + 5 + 11 Le nombre 28 est
le plus petit ayant, au moins, une partition à 2, 3, 4 et 5 termes:
Cette table a été recalculée et rectifiée le
11/05/2023 |
|
|
Merci à Jean-Marc REBERT
pour ses recherches
|
|
||
|
Nombres ayant au moins une partition à deux,
trois, quatre et cinq termes distincts. |
Seul le plus petit exemple de partitions est
donné pour tous les cas jusqu'à 100. Voir exemple avec 28 dont toutes les partitions
en nombres premiers distincts sont indiquées ci-dessus. |
|
|
28, [5,
23], [2, 3, 23], [3, 5, 7, 13], [2, 3, 5, 7, 11] 34, [3,
31], [2, 3, 29], [3, 5, 7, 19], [2, 3, 5, 7, 17] 36, [5,
31], [2, 3, 31], [3, 5, 11, 17], [2, 3, 5, 7, 19] 38, [7,
31], [2, 5, 31], [3, 5, 7, 23], [2, 3, 5, 11, 17] 39, [2,
37], [3, 5, 31], [2, 3, 5, 29], [3, 5, 7, 11, 13] 40, [3,
37], [2, 7, 31], [3, 5, 13, 19], [2, 3, 5, 7, 23] 42, [5,
37], [2, 3, 37], [3, 5, 11, 23], [2, 3, 5, 13, 19] 43, [2,
41], [3, 11, 29], [2, 3, 7, 31], [3, 5, 7, 11, 17] 44, [3,
41], [2, 5, 37], [3, 5, 7, 29], [2, 3, 5, 11, 23] 45, [2,
43], [3, 5, 37], [2, 3, 11, 29], [3, 5, 7, 11, 19] 46, [3,
43], [2, 3, 41], [3, 5, 7, 31], [2, 3, 5, 7, 29] 48, [5,
43], [2, 3, 43], [3, 5, 11, 29], [2, 3, 5, 7, 31] 49, [2,
47], [3, 5, 41], [2, 3, 7, 37], [3, 5, 7, 11, 23] 50, [3,
47], [2, 5, 43], [3, 5, 11, 31], [2, 3, 5, 11, 29] 52, [5,
47], [2, 3, 47], [3,
5, 7, 37], [2, 3, 5, 11, 31] 54, [7,
47], [2, 5, 47], [3, 5, 17, 29], [2, 3, 5, 7, 37] 55, [2,
53], [3, 5, 47], [2, 3, 7, 43], [3, 5, 7, 11, 29] 56, [3,
53], [2, 7, 47], [3, 5, 7, 41], [2, 3, 5, 17, 29] 58, [5,
53], [2, 3, 53], [3, 5, 7, 43], [2, 3, 5, 7, 41] 60, [7,
53], [2, 5, 53], [3, 5, 11, 41], [2, 3, 5, 7, 43] 61, [2,
59], [3, 5, 53], [2, 3, 13, 43], [3, 5, 7, 17, 29] 62, [3,
59], [2, 7, 53], [3, 5, 7, 47], [2, 3, 5, 11, 41] 63, [2,
61], [3, 7, 53], [2, 3, 5, 53], [3, 5, 7, 11, 37] 64, [3,
61], [2, 3, 59], [3, 5, 13, 43], [2, 3, 5, 7, 47] 66, [5,
61], [2, 3, 61], [3, 5, 11, 47], [2, 3, 5, 13, 43] 68, [7,
61], [2, 5, 61], [3, 5, 7, 53], [2, 3, 5, 11, 47] 69, [2, 67],
[3, 5, 61], [2, 3, 5,
59], [3, 5, 7, 11, 43] 70, [3,
67], [2, 7, 61], [3, 5, 19, 43], [2, 3, 5, 7, 53] 72, [5,
67], [2, 3, 67], [3, 5, 11, 53], [2, 3, 5, 19, 43] 73, [2,
71], [3, 11, 59], [2, 3, 7, 61], [3, 5, 7, 11, 47] 74, [3,
71], [2, 5, 67], [3, 5, 7, 59], [2, 3, 5, 11, 53] 75, [2,
73], [3, 5, 67], [2, 3, 11, 59], [3, 5, 7, 13, 47] 76, [3,
73], [2, 3, 71], [3, 5, 7, 61], [2, 3, 5, 7, 59] 78, [5,
73], [2, 3, 73], [3, 5, 11, 59], [2, 3, 5, 7, 61] 80, [7,
73], [2, 5, 73], [3, 5, 11, 61], [2, 3, 5, 11, 59] 81, [2,
79], [3, 5, 73], [2, 3, 5, 71], [3, 5, 7, 13, 53] 82, [3,
79], [2, 7, 73], [3, 5, 7, 67], [2, 3, 5, 11, 61] 84, [5,
79], [2, 3, 79], [3, 5, 17, 59], [2, 3, 5, 7, 67] 85, [2,
83], [3, 11, 71], [2, 3, 7, 73], [3, 5, 7, 11, 59] 86, [3,
83], [2, 5, 79], [3, 5, 7, 71], [2, 3, 5, 17, 59] 88, [5,
83], [2, 3, 83], [3, 5, 7, 73], [2, 3, 5, 7, 71] 90, [7,
83], [2, 5, 83], [3, 5, 11, 71], [2, 3, 5, 7, 73] 91, [2,
89], [3, 5, 83], [2, 3, 7, 79], [3, 5, 7, 17, 59] 92, [3,
89], [2, 7, 83], [3, 5, 11, 73], [2, 3, 5, 11, 71] 94, [5,
89], [2, 3, 89], [3, 5, 7, 79], [2, 3, 5, 11, 73] 96, [7,
89], [2, 5, 89], [3, 5, 17, 71], [2, 3, 5, 7, 79] 98, [19,
79], [2, 7, 89], [3, 5, 7, 83], [2, 3, 5, 17, 71] 99, [2,
97], [3, 7, 89], [2, 3, 5, 89], [3, 5, 7, 11, 73] 100, [3,
97], [2, 19, 79], [3, 5, 13, 79], [2, 3, 5, 7, 83] |
||
|
|
|||||
|
On donne
toutes les possibilités de partitions en carrés de nombres premiers jusqu'à
2500. Lecture: 8 = 2² + 2² ; 12 = 2² + 2² + 2² ; 13 = 2² + 3² ; etc. Records en quantité de
représentations: 12, 219, 363, 699, 1179, 2019, 2259, 3891, 4059,
6459, 5379, 10899, 13179, 10659, 12579, 21819, 20979, 26859, 34419, 38379,
41019, 61299, 39459, 41811, 82131, 50379, 77451, 71379, 141099, 85491,
103971, 74571, 180411, 108339, 179739, 161139, 126819, 225099, … |
|||||
|
8, 2, 2 12, 2, 2, 2 13, 2, 3 17, 2, 2, 3 18, 3, 3 22, 2, 3, 3 27, 3, 3, 3 29, 2, 5 33, 2, 2, 5 34, 3, 5 38, 2, 3, 5 43, 3, 3, 5 50, 5, 5 53, 2, 7 54, 2, 5, 5 57, 2, 2, 7 58, 3, 7 59, 3, 5, 5 62, 2, 3, 7 67, 3, 3, 7 74, 5, 7 75, 5, 5, 5 78, 2, 5, 7 83, 3, 5, 7 98, 7, 7 99, 5, 5, 7 102, 2, 7, 7 107, 3, 7, 7 123, 5, 7, 7 125, 2, 11 129, 2, 2, 11 130, 3, 11 134, 2, 3, 11 139, 3, 3, 11 146, 5, 11 147, 7, 7, 7 150, 2, 5, 11 155, 3, 5, 11 170, 7, 11 171, 5, 5, 11 173, 2, 13 174, 2, 7, 11 177, 2, 2, 13 178, 3, 13 179, 3, 7, 11 182, 2, 3, 13 187, 3, 3, 13 194, 5, 13 195, 5, 7, 11 198, 2, 5, 13 203, 3, 5, 13 218, 7, 13 219, 5, 5, 13 219, 7, 7, 11 222, 2, 7, 13 227, 3, 7, 13 242, 11, 11 243, 5, 7, 13 246, 2, 11, 11 251, 3, 11, 11 267, 5, 11, 11 267, 7, 7, 13 290, 11, 13 291, 7, 11, 11 293, 2, 17 294, 2, 11, 13 297, 2, 2, 17 298, 3, 17 299, 3, 11, 13 302, 2, 3, 17 307, 3, 3, 17 314, 5, 17 315, 5, 11, 13 318, 2, 5, 17 323, 3, 5, 17 338, 7, 17 338, 13, 13 339, 5, 5, 17 339, 7, 11, 13 342, 2, 7, 17 342, 2, 13, 13 347, 3, 7, 17 347, 3, 13, 13 363, 5, 7, 17 363, 5, 13, 13 363, 11, 11, 11 365, 2, 19 369, 2, 2, 19 370, 3, 19 374, 2, 3, 19 379, 3, 3, 19 386, 5, 19 387, 7, 7, 17 387, 7, 13, 13 390, 2, 5, 19 395, 3, 5, 19 410, 7, 19 410, 11, 17 411, 5, 5, 19 411, 11, 11, 13 414, 2, 7, 19 414, 2, 11, 17 419, 3, 7, 19 419, 3, 11, 17 435, 5, 7, 19 435, 5, 11, 17 458, 13, 17 459, 7, 7, 19 459, 7, 11, 17 |
459, 11, 13, 13 462, 2, 13, 17 467, 3, 13, 17 482, 11, 19 483, 5, 13, 17 486, 2, 11, 19 491, 3, 11, 19 507, 5, 11, 19 507, 7, 13, 17 507, 13, 13, 13 530, 13, 19 531, 7, 11, 19 531, 11, 11, 17 533, 2, 23 534, 2, 13, 19 537, 2, 2, 23 538, 3, 23 539, 3, 13, 19 542, 2, 3, 23 547, 3, 3, 23 554, 5, 23 555, 5, 13, 19 558, 2, 5, 23 563, 3, 5, 23 578, 7, 23 578, 17, 17 579, 5, 5, 23 579, 7, 13, 19 579, 11, 13, 17 582, 2, 7, 23 582, 2, 17, 17 587, 3, 7, 23 587, 3, 17, 17 603, 5, 7, 23 603, 5, 17, 17 603, 11, 11, 19 627, 7, 7, 23 627, 7, 17, 17 627, 13, 13, 17 650, 11, 23 650, 17, 19 651, 11, 13, 19 654, 2, 11, 23 654, 2, 17, 19 659, 3, 11, 23 659, 3, 17, 19 675, 5, 11, 23 675, 5, 17, 19 698, 13, 23 699, 7, 11, 23 699, 7, 17, 19 699, 11, 17, 17 699, 13, 13, 19 702, 2, 13, 23 707, 3, 13, 23 722, 19, 19 723, 5, 13, 23 726, 2, 19, 19 731, 3, 19, 19 747, 5, 19, 19 747, 7, 13, 23 747, 13, 17, 17 771, 7, 19, 19 771, 11, 11, 23 771, 11, 17, 19 818, 17, 23 819, 11, 13, 23 819, 13, 17, 19 822, 2, 17, 23 827, 3, 17, 23 843, 5, 17, 23 843, 11, 19, 19 845, 2, 29 849, 2, 2, 29 850, 3, 29 854, 2, 3, 29 859, 3, 3, 29 866, 5, 29 867, 7, 17, 23 867, 13, 13, 23 867, 17, 17, 17 870, 2, 5, 29 875, 3, 5, 29 890, 7, 29 890, 19, 23 891, 5, 5, 29 891, 13, 19, 19 894, 2, 7, 29 894, 2, 19, 23 899, 3, 7, 29 899, 3, 19, 23 915, 5, 7, 29 915, 5, 19, 23 939, 7, 7, 29 939, 7, 19, 23 939, 11, 17, 23 939, 17, 17, 19 962, 11, 29 965, 2, 31 966, 2, 11, 29 969, 2, 2, 31 970, 3, 31 971, 3, 11, 29 974, 2, 3, 31 979, 3, 3, 31 986, 5, 31 987, 5, 11, 29 987, 13, 17, 23 990, 2, 5, 31 |
995, 3, 5, 31 1010, 7, 31 1010, 13, 29 1011, 5, 5, 31 1011, 7, 11, 29 1011, 11, 19, 23 1011, 17, 19, 19 1014, 2, 7, 31 1014, 2, 13, 29 1019, 3, 7, 31 1019, 3, 13, 29 1035, 5, 7, 31 1035, 5, 13, 29 1058, 23, 23 1059, 7, 7, 31 1059, 7, 13, 29 1059, 13, 19, 23 1062, 2, 23, 23 1067, 3, 23, 23 1082, 11, 31 1083, 5, 23, 23 1083, 11, 11, 29 1083, 19, 19, 19 1086, 2, 11, 31 1091, 3, 11, 31 1107, 5, 11, 31 1107, 7, 23, 23 1107, 17, 17, 23 1130, 13, 31 1130, 17, 29 1131, 7, 11, 31 1131, 11, 13, 29 1134, 2, 13, 31 1134, 2, 17, 29 1139, 3, 13, 31 1139, 3, 17, 29 1155, 5, 13, 31 1155, 5, 17, 29 1179, 7, 13, 31 1179, 7, 17, 29 1179, 11, 23, 23 1179, 13, 13, 29 1179, 17, 19, 23 1202, 19, 29 1203, 11, 11, 31 1206, 2, 19, 29 1211, 3, 19, 29 1227, 5, 19, 29 1227, 13, 23, 23 1250, 17, 31 1251, 7, 19, 29 1251, 11, 13, 31 1251, 11, 17, 29 1251, 19, 19, 23 1254, 2, 17, 31 1259, 3, 17, 31 1275, 5, 17, 31 1299, 7, 17, 31 1299, 13, 13, 31 1299, 13, 17, 29 1322, 19, 31 1323, 11, 19, 29 1326, 2, 19, 31 1331, 3, 19, 31 1347, 5, 19, 31 1347, 17, 23, 23 1370, 23, 29 1371, 7, 19, 31 1371, 11, 17, 31 1371, 13, 19, 29 1373, 2, 37 1374, 2, 23, 29 1377, 2, 2, 37 1378, 3, 37 1379, 3, 23, 29 1382, 2, 3, 37 1387, 3, 3, 37 1394, 5, 37 1395, 5, 23, 29 1398, 2, 5, 37 1403, 3, 5, 37 1418, 7, 37 1419, 5, 5, 37 1419, 7, 23, 29 1419, 13, 17, 31 1419, 17, 17, 29 1419, 19, 23, 23 1422, 2, 7, 37 1427, 3, 7, 37 1443, 5, 7, 37 1443, 11, 19, 31 1467, 7, 7, 37 1490, 11, 37 1490, 23, 31 1491, 11, 23, 29 1491, 13, 19, 31 1491, 17, 19, 29 1494, 2, 11, 37 1494, 2, 23, 31 1499, 3, 11, 37 1499, 3, 23, 31 1515, 5, 11, 37 1515, 5, 23, 31 1538, 13, 37 1539, 7, 11, 37 1539, 7, 23, 31 1539, 13, 23, 29 1539, 17, 17, 31 1542, 2, 13, 37 |
1547, 3, 13, 37 1563, 5, 13, 37 1563, 19, 19, 29 1587, 7, 13, 37 1587, 23, 23, 23 1611, 11, 11, 37 1611, 11, 23, 31 1611, 17, 19, 31 1658, 17, 37 1659, 11, 13, 37 1659, 13, 23, 31 1659, 17, 23, 29 1662, 2, 17, 37 1667, 3, 17, 37 1682, 29, 29 1683, 5, 17, 37 1683, 19, 19, 31 1685, 2, 41 1686, 2, 29, 29 1689, 2, 2, 41 1690, 3, 41 1691, 3, 29, 29 1694, 2, 3, 41 1699, 3, 3, 41 1706, 5, 41 1707, 5, 29, 29 1707, 7, 17, 37 1707, 13, 13, 37 1710, 2, 5, 41 1715, 3, 5, 41 1730, 7, 41 1730, 19, 37 1731, 5, 5, 41 1731, 7, 29, 29 1731, 19, 23, 29 1734, 2, 7, 41 1734, 2, 19, 37 1739, 3, 7, 41 1739, 3, 19, 37 1755, 5, 7, 41 1755, 5, 19, 37 1779, 7, 7, 41 1779, 7, 19, 37 1779, 11, 17, 37 1779, 17, 23, 31 1802, 11, 41 1802, 29, 31 1803, 11, 29, 29 1806, 2, 11, 41 1806, 2, 29, 31 1811, 3, 11, 41 1811, 3, 29, 31 1827, 5, 11, 41 1827, 5, 29, 31 1827, 13, 17, 37 1850, 13, 41 1851, 7, 11, 41 1851, 7, 29, 31 1851, 11, 19, 37 1851, 13, 29, 29 1851, 19, 23, 31 1853, 2, 43 1854, 2, 13, 41 1857, 2, 2, 43 1858, 3, 43 1859, 3, 13, 41 1862, 2, 3, 43 1867, 3, 3, 43 1874, 5, 43 1875, 5, 13, 41 1878, 2, 5, 43 1883, 3, 5, 43 1898, 7, 43 1898, 23, 37 1899, 5, 5, 43 1899, 7, 13, 41 1899, 13, 19, 37 1899, 23, 23, 29 1902, 2, 7, 43 1902, 2, 23, 37 1907, 3, 7, 43 1907, 3, 23, 37 1922, 31, 31 1923, 5, 7, 43 1923, 5, 23, 37 1923, 11, 11, 41 1923, 11, 29, 31 1926, 2, 31, 31 1931, 3, 31, 31 1947, 5, 31, 31 1947, 7, 7, 43 1947, 7, 23, 37 1947, 17, 17, 37 1970, 11, 43 1970, 17, 41 1971, 7, 31, 31 1971, 11, 13, 41 1971, 13, 29, 31 1971, 17, 29, 29 1974, 2, 11, 43 1974, 2, 17, 41 1979, 3, 11, 43 1979, 3, 17, 41 1995, 5, 11, 43 1995, 5, 17, 41 2018, 13, 43 2019, 7, 11, 43 2019, 7, 17, 41 2019, 11, 23, 37 |
2019, 13, 13, 41 2019, 17, 19, 37 2019, 23, 23, 31 2022, 2, 13, 43 2027, 3, 13, 43 2042, 19, 41 2043, 5, 13, 43 2043, 11, 31, 31 2043, 19, 29, 29 2046, 2, 19, 41 2051, 3, 19, 41 2067, 5, 19, 41 2067, 7, 13, 43 2067, 13, 23, 37 2091, 7, 19, 41 2091, 11, 11, 43 2091, 11, 17, 41 2091, 13, 31, 31 2091, 17, 29, 31 2091, 19, 19, 37 2138, 17, 43 2139, 11, 13, 43 2139, 13, 17, 41 2142, 2, 17, 43 2147, 3, 17, 43 2163, 5, 17, 43 2163, 11, 19, 41 2163, 19, 29, 31 2187, 7, 17, 43 2187, 13, 13, 43 2187, 17, 23, 37 2210, 19, 43 2210, 23, 41 2210, 29, 37 2211, 13, 19, 41 2211, 17, 31, 31 2211, 23, 29, 29 2213, 2, 47 2214, 2, 19, 43 2214, 2, 23, 41 2214, 2, 29, 37 2217, 2, 2, 47 2218, 3, 47 2219, 3, 19, 43 2219, 3, 23, 41 2219, 3, 29, 37 2222, 2, 3, 47 2227, 3, 3, 47 2234, 5, 47 2235, 5, 19, 43 2235, 5, 23, 41 2235, 5, 29, 37 2238, 2, 5, 47 2243, 3, 5, 47 2258, 7, 47 2259, 5, 5, 47 2259, 7, 19, 43 2259, 7, 23, 41 2259, 7, 29, 37 2259, 11, 17, 43 2259, 17, 17, 41 2259, 19, 23, 37 2262, 2, 7, 47 2267, 3, 7, 47 2283, 5, 7, 47 2283, 19, 31, 31 2307, 7, 7, 47 2307, 13, 17, 43 2330, 11, 47 2330, 31, 37 2331, 11, 19, 43 2331, 11, 23, 41 2331, 11, 29, 37 2331, 17, 19, 41 2331, 23, 29, 31 2334, 2, 11, 47 2334, 2, 31, 37 2339, 3, 11, 47 2339, 3, 31, 37 2355, 5, 11, 47 2355, 5, 31, 37 2378, 13, 47 2378, 23, 43 2379, 7, 11, 47 2379, 7, 31, 37 2379, 13, 19, 43 2379, 13, 23, 41 2379, 13, 29, 37 2382, 2, 13, 47 2382, 2, 23, 43 2387, 3, 13, 47 2387, 3, 23, 43 2403, 5, 13, 47 2403, 5, 23, 43 2403, 19, 19, 41 2427, 7, 13, 47 2427, 7, 23, 43 2427, 17, 17, 43 2427, 23, 23, 37 2451, 11, 11, 47 2451, 11, 31, 37 2451, 23, 31, 31 2498, 17, 47 2499, 11, 13, 47 2499, 11, 23, 43 2499, 13, 31, 37 2499, 17, 19, 43 2499, 17, 23, 41 2499, 17, 29, 37 |
|
![]()
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()