|
Édition du: 31/08/2022 |
|
INDEX |
Frontières |
||
Faites un double-clic pour un retour en haut de page
![]()
|
FRONTIÈRE COMMUNE à plusieurs pays Serait-il possible de redessiner la carte du
monde de façon à ce que tous les pays aient une seule et unique frontière
(ou, en d’autres termes, exactement la même frontière) ? Il existe une méthode simple pour répondre à
cette question. Celle-ci a été décrite en 1917 par le
mathématicien japonais Kunizo Yoneyama, qui attribue sa découverte à son
professeur Takeo Wada. Elle nécessite de passer aux limites … |
||
|
|
Sommaire de cette page >>> Frontière commune entre deux pays >>> Frontière commune entre trois pays >>> Historique |
Débutants Glossaire |
|
Deux pays voisins non-insulaires sont séparés par
une frontière commune. |
Prenons une Terre imaginaire sans océan.
L'hémisphère nord est un pays. L'hémisphère sud un autre. La frontière commune est l'équateur. Placé à proximité de l'équateur, il suffit d'un
pas pour passer d'un pays à 'autre. |
|
|
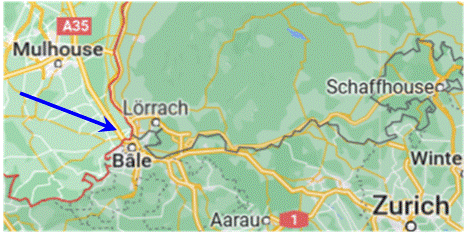
Avec trois pays, il existe au mieux un point
triple commun. C'est le cas pour la France, l'Allemagne et la
Suisse, par exemple. |
|
|
|
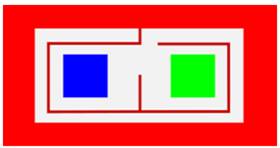
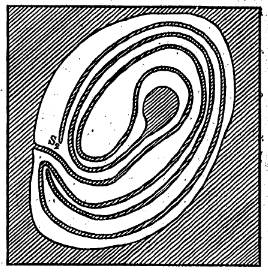
Pour obtenir une frontière commune entre trois
pays, la méthode consiste à partir d'une situation et de la faire évoluer
jusqu'à l'infini. À chaque itération, la frontière de chaque pays
est étendue dans la zone blanche non encore attribuée. À la deuxième étape, le pays rouge s'étend sous
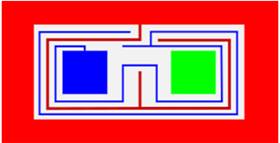
la forme d'un territoire étroit. Puis, le territoire bleu fait de même selon le
tracé indiqué. Le procédé va se poursuivre selon le même
principe. Progressivement la zone blanche est annexée par
chacun des trois pays. Après un nombre infini d’étapes, la construction
de Wada converge vers une frontière très fine. On obtient ainsi trois pays, les pays rouge, bleu
et vert qui serpentent l’un autour de l’autre et une zone blanche qui est
infiniment étroite. C’est ainsi que la zone blanche finale va former
une ligne de séparation des trois pays ou, autrement dit, la frontière
commune du pays rouge, bleu et vert. |
Situation de départ: trois pays et
une zone blanche
Deuxième étape
Étape n
|
|
Source des figures Article
de Iakovogloucité en bas de page
|
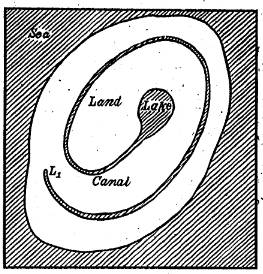
Cette construction a été décrite en 1917 par le
mathématicien japonais Kunizo Yoneyama, qui attribue sa découverte à son
professeur Takeo Wada. Yoneyama décrivit le résultat non pas en termes
de pays séparés par des frontières, mais plutôt en termes de lacs séparés par
des portions de terre. C’est ainsi qu’aujourd’hui des pays avec exactement la
même frontière sont appelés en mathématiques des lacs de Wada. Malgré leur nature surprenante, de nos jours, les
lacs de Wada apparaissent
naturellement dans l’étude des systèmes chaotiques. Figures extraites de l'article
original (pdf 16 pages – Niveau
avancé) Theory of
Continuous Set of Points –
Kunizo Yoneyama
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |