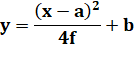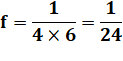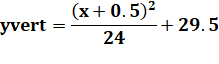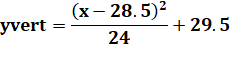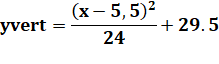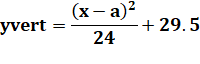|
Édition du: 30/04/2022 |
|
INDEX |
Paraboles |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Paraboles et nombres premiers Étude d'une
formule en x² produisant une suite de nombres premiers. Pourquoi prend-elle
plusieurs formes ? Il s'agit simplement des mêmes formules, mais décalées. |
||
|
|
Sommaire de cette page >>> Le sujet … >>> Examen des formules >>> Examen des paraboles |
Débutants Glossaire |
|
On
trouve celle-ci dans les listes de formules de Wolfram
Mathworld et sur ma
page des formules produisant des suites de nombres premiers. Elle
est aussi en A168028. |
6x² – 342 + 4903 |
||
|
La
suite A060844 propose une formule plus
simple. Un
internaute, adepte de mathématiques, Louis-Marie Genet, propose aussi cette
formule qui produit les mêmes nombres avec une formule plus simple. |
6x² – 6x + 31 |
||
|
Voyons
les différences ! |
Et
concluons qu'effectivement la formule est plus simple, et elle offre un
calcul plus rapide et sans doublons. |
||
|
Formule 6x² – 6x + 31 |
31,
43, 67, 103, 151, 211, 283, 367, 463, 571, 691, 823, 967, 1123, 1291, 1471,
1663, 1867, 2083, 2311, 2551, 2803, 3067, 3343, 3631, 3931, 4243, 4567, 4903,
5251 |
|
|
Formule 6x² + 6x + 31 |
Même
liste à l'exception du 31, manquant. |
|
|
Formule 6x² – 342 + 4903 Oui,
mais nombreux doublons ! Un exemple en rouge. |
4567, 4243,
3931, 3631, 3343, 3067, 2803, 2551, 2311, 2083, 1867, 1663, 1471, 1291, 1123,
967, 823, 691, 571, 463, 367, 283, 211, 151, 103, 67, 43, 31, 31, 43, 67,
103, 151, 211, 283, 367, 463, 571, 691, 823, 967, 1123, 1291, 1471, 1663,
1867, 2083, 2311, 2551, 2803, 3067, 3343, 3631, 3931, 4243, 4567, 4903, 5251 |
|
|
Ensemble
sans doublons |
{31,
43, 67, 103, 151, 211, 283, 367, 463, 571, 691, 823, 967, 1123, 1291, 1471,
1663, 1867, 2083, 2311, 2551, 2803, 3067, 3343, 3631, 3931, 4243, 4567, 4903,
5251} |
|
|
Conclusions Les
deux formules sont équivalentes. |
6x² – 6x + 31 6x² – 342x + 4903 |
|
|
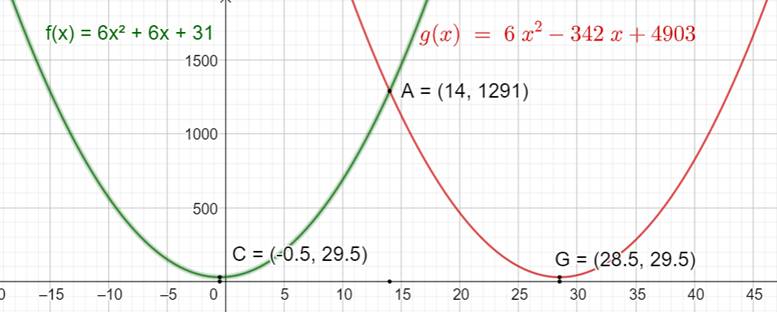
Comparaison des deux paraboles représentatives des fonctions
Ce
sont deux paraboles de même forme (même évasement), mais décalées en abscisses. Pas
étonnant de trouver les mêmes valeurs en ordonnées, certes avec des x
différents. La
courbe rouge montre également pourquoi le calcul donne deux fois la même
valeur en ordonnée. La
première formule (parabole verte) serait donc plus économe en calcul. |
||
|
Peut-on décaler la parabole à loisir ? Il
faut pour cela revenir à la fonction
canonique de la parabole. |
6x² +
6x + 31 6x² –
342 + 4903 |
|
|
Parabole verticale y
est l'ordonnée du foyer; (a,
b) sont les coordonnées du sommet (le point bas de la parabole). |
|
|
|
Ordonnée du foyer Au
¼ de l'inverse du coefficient de x². Elle
caractérise l'évasement de la parabole. |
|
|
|
Première formule Coordonnées
du sommet C: |
|
|
|
Deuxième formule Coordonnées
du sommet G: |
|
|
|
Autre formule Coordonnées
du sommet: |
|
|
|
Liste des premiers avec
cette formule La
même liste des 30 nombres premiers avec 5 doublons. Plus
la courbe sera décalée vers la droite, plus il y aura de doublons. |
31,
43, 67, 103, 151, 211, 283, 367, 463, 571, 691, 823, 967, 1123, 1291, 1471,
1663, 1867, 2083, 2311, 2551, 2803, 3067, 3343, 3631, 3931, 4243, 4567, 4903,
5251 |
|
|
Conclusion Toutes
ces formules avec a = (un entier + 1/2) produiront les 30 nombres premiers de la
liste initiale. |
|
|
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/ParaPrem.htm
|
|