|
NOMBRES -
Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Références / Nouveautés ORIENTATION GÉNÉRALE - M'écrire - Édition du: 01/10/2005 |
|
-Ý- FAQ - Foire
aux Questions |
||||
|
ARITHMÉTIQUE |
/ Constantes |
|
|
|
|
Sur cette page >>> Pi est-il INCOMMENSURABLE
? >>> QUADRATURE DU CERCLE & CALCUL de Pi |
Pages Générales §
Théorie des
nombres - Index §
Calcul §
Logique §
Humour |
|||
|
FAQ
- Pour commencer votre lecture sur le même sujet >>> ON MESURE TRÈS FACILEMENT PI, ALORS POURQUOI
TANT D'HISTOIRES |
|
Pi est-il INCOMMENSURABLE ? Question Je ne parviens pas à croire malgré toutes les démonstrations de génies mathématiques et les calculs de nos super-ordinateurs que Pi soit infini car c'est tout bonnement impossible. Si on multiplie le rayon par un chiffre infini, on devrait obtenir une aire ou un périmètre infini, ce qui n'est pas le cas. Il y a donc quelque chose qui heurte le sens. Réponse Attention à ne pas confondre les types d'infinis C'est la quantité de chiffres après la virgule qui est infinie, et non pas la valeur du nombre Essayons d'y voir plus
clair: Dans notre système de numération de position, plus un chiffre est loin de la virgule moins il "pèse": en 3e position il vaut 1/1000 et, en 6e position il ne vaut plus que 1 /1000 000 Lorsqu'on ajoute des chiffres loin derrière la virgule, il ne valent plus grand chose Lorsqu'on cherche plus de décimales, on fignole en quelque sorte! Pour Pi, sa valeur reste voisine de 3,14 En fait: jamais plus petit que 3,14, mais jamais plus grand que 3,15 donc loin d'être infini en valeur Question Pi malgré son grand charme mystérieux n'est, après tout, qu'un pourcentage de 4. Car 3,1416 / 4 = 78,54%, rapport du cercle au carré dans lequel il est circonscrit. Il n'est donc pas VRAIMENT un concept incommensurable (me dis-je) Réponse D'abord, il vaudrait mieux écrire: avec 2 décimales: 3,14… / 4 = 78,53 …% avec 4 décimales: 3,1415… / 4 = 78,5398 …% Je pense que le mot incommensurable (pas mesurable franchement) est déroutant On utilise aujourd'hui le mot irrationnel (pas de ration franche) Que l'on ne peut pas partager nettement, franchement Que l'on ne peut pas représenter sous la forme d'une fraction, ni d'un pourcentage net Essayons d'y voir plus clair: Il existe au moins trois races de partages (pour ce qui concerne notre propos) §
Partage net de chez net Partage en moitié: fraction 1/2 ou, exprimé en décimal 0,5 § Partage simplement net, mais il ne faut pas y regarder de trop près Partage en
tiers: fraction 1/3 et en décimal 0,333333333…une infinité de 3 Partage pas complètement net, car une infinité de décimales Plus je veux de précision, plus je dois prendre de 3 §
Partage non net Prenons le partage de la diagonale du carré par son côté Ce rapport vaut Racine de 2 Soit 1,41421356….une infinité de chiffres différents Ou encore 141,421356….infinité de chiffres différents en % Ce rapport ne peut pas s'exprimer sous la forme d'une fraction Comme beaucoup de nombres, Pi appartient à cette catégorie de nombres dits IRRATIONNELS Plus on veut de précision, plus il faut ajouter de décimales Il n'y a pas de fraction pour les représenter avec une précision infinie (comme on le fait avec 1/2 ou 1/3) Question Donc je continue à être obsédée
par Pi...et à chercher des renseignements. Je n'ai pas trouvé la
démonstration qui donne Pi égal à 3,1416...et quelques millions de
poussière de chiffres. Réponse Un cercle est en fait un polygone régulier ayant une infinité de côtés On connaît exactement la valeur du périmètre d'un polygone régulier en fonction de la longueur du côté On calcule le périmètre d'un polygone qui a de plus en plus de côtés Plus, on considère de côtés et plus on obtient une valeur proche de celle de Pi Pour vous rassurer sur le caractère limité du nombre Pi, je dois dire que même les Anciens avaient imaginé de calculer la valeur par défaut et la valeur par excès Il prenaient deux polygones, l'un intérieur au cercle et l'autre extérieur Ils obtenaient ainsi un encadrement de la valeur de Pi Les méthodes de calcul sont aujourd'hui plus sophistiquées mais procèdent du même principe Dans la pratique, on n'a jamais besoin de plus de 10 à 20 décimales, ce qui correspond déjà à une précision hallucinante Ce sont les mordus de théorie des nombres qui calculent tant de décimales. Ils tentent de déceler une forme particulière dans Pi: comme par exemple: est-ce que tous les chiffres de 0 à 9 se retrouvent également répartis parmi toutes ces décimales Question Est-ce que le centre d'un carré se trouve bien à l'intersection des diagonales allant d'un angle à l'angle opposé? Est-ce que la distance moyenne du centre d'un carré de superficie quelconque par rapport à tous les points du carré est la même que celle de la distance moyenne du centre de n'importe quelle figure géométrique de même surface à tous les points de cette figure? Réponse Le centre du carré est bien le point d'intersection des diagonales du carré C'est aussi le centre de gravité (en gros, la matière est répartie uniformément autour de ce point, et suspendu par ce point, le carré restera horizontal) Pour le cercle, c'est son centre qui joue ce rôle Toutes les figures et tous les volumes ont un centre de gravité. Il est parfois difficile à déterminer lorsque l'objet est irrégulier: il se trouve dans l'alignement du fil qui vous sert à le pendre. Question On divise un carré par ses diagonales et ses médiatrices, ce qui donne 8 triangles rectangles (…) Pourquoi le rapport du carré de l'hypoténuse d'un de ces triangles rectangles à la superficie du carré est-il toujours de 3,20? Cela peut-il avoir un rapport (!!!) avec Pi? Réponse Je suis un peu embarrassé, car je ne vois pas d'où vient ce 3,20 En tout cas soyez certaine, il n'y a pas de rapport avec Pi Voyons, ce que j'ai compris,
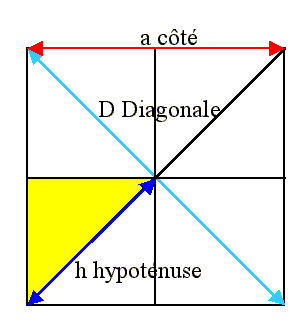
et le calcul correspondant Si j'ai bien compris, voici le dessin Vous avez calculé le rapport h² / a²
Calculons h h = 1/2 D h² = 1/4 D² D² = a² + a² (théorème de
Pythagore) D² = 2 a² h² = (1/4) (2a²) = 1/2 a² Et finalement votre rapport h² / a² = (1/2 a²) / a² = 1/2 = 0,5 Pour poursuivre vos recherches Sur Pi http://villemin.gerard.free.fr/NombDico/FAQ1/Constant.htm#quadra Sur les rationnels http://villemin.gerard.free.fr/Wwwgvmm/Type/NbDebut.htm |
|
|
|
|
Rubrique QUADRATURE DU CERCLE & CALCUL de Pi Question J'ai cherché comment calculer la surface d'un cercle sans utiliser le nombre Pi. Je trace un carré dans lequel est inscrit un cercle.
Je constate tout de suite que le carré est plus grand que le cercle. Je me
dis donc qu'il faut enlever un pourcentage de l'aire du carré pour trouver
l'aire du cercle. J'ai essayer de calculer ce pourcentage. Après beaucoup de
calculs, je l'ai trouvé. Pour trouver l'aire du cercle, il faut faire : Aire du cercle = (2r)² -
21.46018366%. Pourtant, mon cousin ingénieur me dit que 0,214… = (4 - Pi)/4 Qui a raison: avec ou sans Pi ? Réponse 1) D'abord j'apprécie beaucoup la passion et les recherches C'est la seule façon de sentir les choses et de progresser sur du solide Mille fois bravo ! Cependant, le cousin a raison; mais toi aussi Voyons pourquoi 2) COMPARAISON À LA THÉORIE DU CERCLE Cette formule s'écrit en fait A = (2r)² ( 1 - 0,214…) Or l'aire du cercle est égale à S = 3,14… r² = (4 -
0,86…)r² = 4 r² (1 - 0,214…) Calcul du nombre: S = Pi. r² = 4 r² (1
- 0,214…) Pi = 4 (1 - 0,214…) 0,214… = (4 - Pi) /
4 = 1 - Pi/4 On trouve bien ton nombre Pour ton info (avec 100 chiffres): Pi = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 862803482 5342117068 1 - Pi/4 = 0,2146018366 0255169038 4339154180 1242789507 0765015622 3544756263 8519230458 9842844775 0342991293 6644707330 À comparer au nombre que tu as trouvé: pas mal ton calcul ! Mais le cousin a raison: l'ombre de Pi est caché à l'intérieur de ton nombre Normal, il est ingénieur comme moi … Mais, pour l'instant, on a un peu l'impression de tourner en rond … sur le cercle 3) VOYONS JUSTEMENT LE CALCUL de Pi C'est joli de dire que l'aire du cercle est S = Pi . r² Mais, comment calculer la valeur de Pi C'est là où tu as raison, il faut bien trouver un truc Et tu en as trouvé un. Il y a plusieurs grandes classes de types de calcul a) Il y a la méthode égyptienne: elle consiste à partir d'un carré (tiens, tiens…) et, à retirer des carrés ou des morceaux de carrés (triangles) Voir en http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiHistor.htm#Egypte b) Il a la méthode des polygones: elle consiste à calculer l'aire des 2 polygones intérieur et extérieur au cercle. On obtient de plus en plus de décimales justes pour Pi en augmentant la quantité de côtés Voir en http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiCalcul.htm#Polygone c) Il a les méthodes utilisant des formules répétitives ( que l'on appelle des développements) . Plus on répète la formule plus on obtient de décimales de Pi Ce sont ces méthodes qui donnent des records de calcul de décimales Aujourd'hui, on connaît plus de 50 milliards de chiffres dans Pi Voir en Même page que ci-dessus 4) NATURE DE Pi Quelle que soit la manière de s'y prendre, on ne trouvera jamais - ni toutes les décimales de Pi - ni une fraction, car Pi est irrationnel (démonstration Lambert 1761): ce qui veut dire que les décimales de Pi se sont pas répétitives - ni une solution d'une équation, car Pi est transcendant (démonstration Lindemann 1882): ce qui veut dire qu'il n'existe pas de formule permettant de décrire Pi (sauf des formules répétitives sans fin, les développements) On se pose bien d'autres question sur Pi: est-il normal ? On ne sait pas: on ne sait pas si les décimales sont statistiquement bien réparties: autant de 1 que de 2 que de 3 … Voir Propriétés de Pi 5) POUR POURSUIVRE Si tu ne connais pas encore, je pense que les fractions continues (fractions à étage) devraient t'intéresser Elles permettent de représenter Pi (et les autres nombres qui ne se laissent pas faire) de façon élégante et de trouver tout un tas de fractions de plus en plus précises pour les représenter Voir en http://villemin.gerard.free.fr/Wwwgvmm/Nombre/FracCont.htm Pour finir, si tu veux vraiment faire le tour de Pi et de tout ce qui l'entoure (comment on a trouvé tout cela, tentatives de calculs et de constructions de Pi à la règle et au compas …), je te conseille un livre génial et abordable: Le fascinant nombre Pi Jean-Paul Delahaye (le Hubert Reeves des maths) Pour la Science - Belin - 1997 220 pages |
|
§
Cercle |