Carrés magiques multiples (ordre 3) et leur produit magique

Édition du: 08/01/2023

INDEX Carrés magiques Ordres Constructions Jeux de grilles Jeux et énigmes	Carrés magiques 3 x 3
	Intro. carré 3 x 3	Carré 3 x 3	Date de naissance	Fibonacci
	Propriétés	Premiers	Maths du carré 3x3	Décalé
	Maths et programmation		Alpha-magique	Taneja (Pythagore)
			Retourné	Multiple

Faites un double-clic pour un retour en haut de page

Carrés magiques multiples

et leur multiplication

Que deviennent les carrés magiques considérés comme des matrices lorsqu'on les porte à une puissance ou lorsqu'on les multiple entre eux ?

Note: il ne s'agit pas de carrés magiques purs: on a toujours les mêmes sommes sur les lignes, les colonnes et les diagonales. Les nombres doivent être distincts mais pas forcément compris entre 1 et n².

Sommaire de cette page

>>> Carré magique au carré et au cube

>>> Multiplication de deux carrés magiques

>>> Multiplication de trois carrés magiques

Débutants

Carrés magiques

Glossaire

Carrés magiques

Carré magique au carré et au cube			haut
Le carré A est magique. On calcule le carré (A2) en multipliant A par A, la méthode est expliquée ci-dessous Le carré A2 = A ٠A est semi-magique (sans les diagonales) et il n'est guère intéressant. Le troisième, le cube du premier, est entièrement magique et les nombres sont bien tous différents.		Constante magique de A = 15 ; de A2 = 225 ; de A3 = 3375
On retrouve les mêmes propriétés avec: A6 (A à la puissance 6) qui est semi-magique. A9 (A à la puissance 9) est complètement magique.	Constante magique de A6 = 111 390 625 ; de A² = 38 443 359 375.

Source Phil Hobbs et Clifford Pickover

Multiplication de deux carrés magiques		haut
Deux carrés magiques particuliers 4 x 4: A et B. Dans ces carrés, on trouve tous les nombres de – 7 à 7, plus 0 et 8.
Produit des deux matrices. Le calcul sera étudié plus bas. Ce carré est magique de constante 4.	*M = A* ٠ *B =*

Source Réseaux sociaux

Multiplication de trois carrés magiques

haut

Trois carrés magiques 3 x 3 de constantes: 369, 48 et 51.

Produit de deux carrés

On considère les deux premiers carrés comme des matrices.

Et, on effectue leur multiplication:
M = A ٠ B

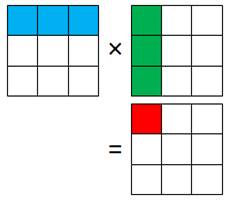
Multiplication de matrices

Rappel de la méthode:

Somme des couples bleus × verts et résultat en rouge. Même principe pour les autres cellules.

Exemples

M[1, 1] = 93 × 12 + 155 × 19 + 121 × 17

= 6 118

M[1, 2] = 93 × 21 + 155 × 16 + 121 × 11

= 5 764.

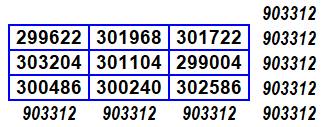
Tous calculs faits pour

M = A ٠ B.

Notez que les nombres sont répétés et qu'il s'agit d'un carré semi-magique (sans les diagonales) de somme 17 712.

Multiplication de cette matrice par C:

N = M ٠ C = A ٠ B ٠ C

Le carré produit est magique

N = A ٠ B ٠ C

Finalement, les carrés N, A, B et C sont magiques.

Source John D. Cook

Haut de page (ou double-clic)

Retour	Carrés magiques d'ordre 3
Suite	Propriétés du carré magique 3x3 Le carré 3 x 3 chinois Cubes magiques Carré 4 x 4	Carrés magiques – Index Grille 3x3 à somme maximale Carré alpha-magique 3x3
Voir	Algorithmes Bi, tripartitions Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour	Jeux Jeux de chiffres Nombres consécutifs Nombres magiques – Index Pannumérique Rubick's cube Rubriques débutants Sudoku
Sites	Magic squares as matrices – John D. Cook
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMord3MU.htm