|
Édition du: 30/12/2023 |
|
INDEX |
Géométrie 3D – POLY- |
|||
|
|
||||
|
|
||||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
HOLYÈDRES Sorte de
polyèdre troué. Un trou en forme de
polygone par face, sans point commun avec les arêtes du polyèdre. |
||
|
|
Sommaire de cette page >>> Holyèdre >>> Cube troué >>> Première solution >>> Solution minimale |
Débutants Glossaire |
|
Définition Un holyèdre est objet géométrique
tridimensionnel. C'est un polyèdre dont chacune des faces contient
au moins un trou en forme de polygone, et dont les limites des trous ne
partagent aucun point entre elles ou avec la limite de la face. Invention Le concept a été introduit pour la première fois
par John H. Conway. Le terme "holyèdre" a été inventé par David W. Wilson en 1997 en tant que mot-valise
entre polyèdres et des trous. Conway a offert un prix de 10 000 USD, pour leur
découverte, somme à diviser par le nombre de faces, incitant à trouver la
solution minimale. |
Historique Existe-t-il un polyèdre dans l'espace
tridimensionnel euclidien qui n'a qu'un nombre fini de faces planes, dont
chacune est un sous-ensemble connexe fermé du plan approprié dont l'intérieur
relatif dans ce plan est connecté de manière multiple ? En 1999, Jade P.
Vinson est le premier a présenter un holyèdre avec 78 585 627 faces. En 2003, Don Hatch réussit à trouver un holyèdre à
seulement 492 faces. |
|
Voir Brève
49-962
|
Exemple pour illustrer le concept Un cube est troué sur chaque face par un trou en
forme de carré. Cet objet ne répond pas à la définition, car chaque
trou d'une face doit transpercer le cube indépendamment les uns des autres. Oui, on peut les décaler et perforer les faces
comme des barres plantées dans le cube sans que les unes touchent les autres. Cependant … Chaque face doit être trouée ! Oups ! En perforant, le cube, d'autres faces sont
crées: ici, seize faces en plus. Comment les perforer à nouveau ? Possible comme pour l'éponge
de Menger. Mais, à chaque itération, le même problème
persiste. On passe effectivement dans le mode des fractales. |
Exemple
Ce cube troué comporte 4 + 4 × 4 = 20 faces. Éponge de Menger
|
|
|
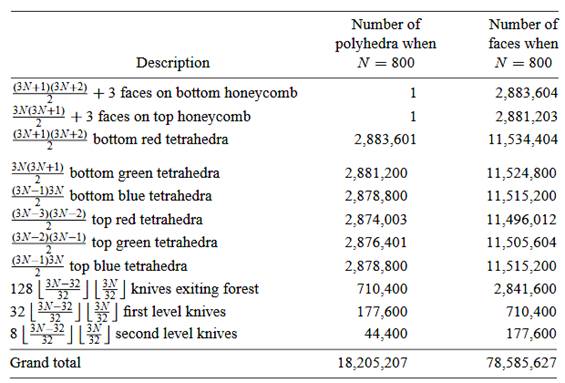
La solution initiale de J. Vince est composée de 78 585 627 faces pour
18 205 207 polyèdres de différents types. Le tableau ci-contre donne une idée de la complexité de cet objet. |
Holyèdre
Source: On holyhedra
– J. Vinson |
|
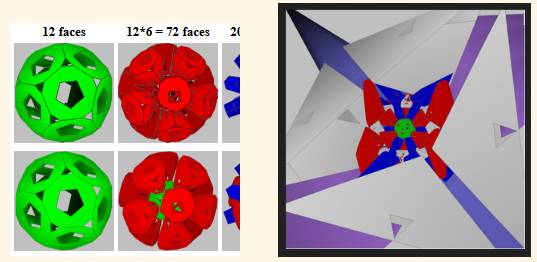
|
La solution de Don Hatch Vince est composée de 492 faces. Ce holyèdre comporte neuf couches. À, gauche les deux premières couches. En haut la couche élémentaire, et en bas la superposition
des couches. À droite, l'holyèdre complet. |
Holyèdre à 492 faces Source: Holyhedron
! – Don Hatch |
|
Anlais
|
A holyhedron is a polyhedron so that the interior
of every face is nonsimply connected. |
Voir
Anglais pour le bac et pour les affaires
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |